<div class="text-justify">
<div class="pull-left"><img src="https://cdn.steemitimages.com/DQmaYhcySoz6fHcuYzAgdyCVH811VJoZevoeZqhsi161fFa/IntegracionPortada.png"><center><sub>Imagen editada con GIMP, gráficos hechos con GNU Octave. Elaborada por @abdulmath.</sub></center></div> Saludos queridos lectores, bienvenidos nuevamente a mi Blog. Quiero compartir con ustedes un nuevo tema en mi blog, siguiendo la línea de análisis numérico, en esta oportunidad comenzaremos a desarrollar un poco el tema de <b>Integración Numérica</b>, usando <b>GNU Octave</b>, en el que hablaremos acerca de las Reglas Compuestas de Integración, Error, mostraremos algunas script y construiremos funciones para mostrar algunos ejemplos. La misma está dirigida al público en general, con destrezas en temas de análisis real, cálculo avanzado, entre otros; con especial énfasis en profesionales y estudiantes universitarios de ciencias, ingeniería y carreras afines. Al final, dejaremos bibliografía, para que puedan consultar algunos tópicos especiales para los interesados. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.

<hr>
<center>https://cdn.steemitimages.com/DQmSFSZja9vPGd5oJjxjxqGAtwXaAwASvsQ1ky5Q6UTwGvQ/Matematicas01.png</center>
<hr>

<h1><div class="phishy">Reglas Compuestas</div></h1>

Continuando con el tema de Integración Numérica, podemos resaltar que la cota del error que describimos en la publicación anterior <a href="https://steemit.com/steemstem/@abdulmath/integracion-numerica-con-gnu-octave-or-1era-parte">Integración Numérica con GNU Octave | 1era Parte</a> salvo el que intervalo o dominio donde queremos acotar sea bastante pequeño, es decir, que <b>h = b - a</b> lo suficientemente pequeño, la misa no es muy buena. Afortunadamente, hay una manera más sencillo o fácil de organizar el cálculo de la integral, de modo que las cuadraturas de intervalos pequeños prevalezcan. A esto se le llama o conoce como <b>Reglas Compuestas</b>.

<hr>
https://cdn.steemitimages.com/DQmaoG5ZuMgFaYHr5CGwe3cA8GVEfH1edL4VwPT3fn1NCtb/SeparadorGMath38.png
<hr>

<h3><div class="phishy">Derivación</div></h3>

Si tenemos una partición
<center>
https://cdn.steemitimages.com/DQmWUpufFQZvr9Vnt1w5zN1VxQhueRKo9kARwBro2iaySmz/ec29.png</center>
entnces
<center>
https://cdn.steemitimages.com/DQmRea31gk6VViysMs1Bb53Skh6NWBuTbJLrbspdpPC1NKN/ec30.png</center>

Si aplicamos <b>Q<sub>NC</sub>(m)</b> a cada una de las subintegrales, resulta una regla de cuadratura compuesta basada en <b>Q<sub>NC</sub>(m)</b>. Por ejemplo, si 
<center>
https://cdn.steemitimages.com/DQmX4fx9r4qEb5nj62H4W7ThvS5Cv8puCShfBVRt6QA9k7S/ec31.png</center>
entonces
<center>
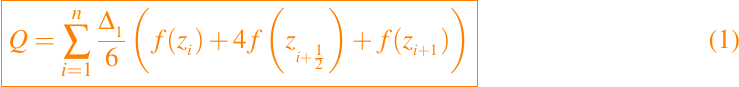![ec32.png](https://cdn.steemitimages.com/DQmRREY75CNEXUw7pWU1kc7x1N1eUzVzyz9pd3cdmHnCg5e/ec32.png)</center>
es una regla compuesta de Simpson. En general, si <b>z</b> esta contenida en una partición de <b>[a, b]</b> y ```fname``` es una cadena de caracteres de alguna función, entonces
<center>
https://cdn.steemitimages.com/DQmeL8vYAHfNN3jpSAAUyv8bsRTxmaftCf3rUTtAiKwageJ/ec33.png
<sub>Script para calcular el valor de <b>Q</b>. Elaborado con GNU Octave, por @abdulmath.</sub></center>
asignamos a ```numI``` la estimación compuesta de <b>m</b> puntos de Newton-Cotes de la integral basada en la partición donde se encuentra <b>z</b>. Más adelante, mostraremos como automatizar la elección de una buena partición. Por ahora nos centraremos en describir reglas compuestas que están basadas en particiones uniformes. En estas reglas, <b>n > 1</b>,
<center>
https://cdn.steemitimages.com/DQmbsXx4tVGicCk6wQtLwgYrrpXRAyAE9pRy4ZaUsQ5AWNA/ec34.png</center>
Para <b>i = 1: n + 1</b>, la regla de evaluación compuesta toma la forma
<center>
https://cdn.steemitimages.com/DQmVrHEKGpfHn4aB17SaVE2zbKKsEKk6wBFzfhr5FQpjxdJ/ec35.png
<sub>Script para evaluar la regla compuesta. Elaborado con GNU Octave, por @abdulmath.</sub></center>

Designemos la estimación producida por la regla de cuadratura mediante <b>Q<sup>(n)</sup><sub>NC</sub>(m)</b>.  El cálculo es un poco ineficiente ya que se involucra <b>n - 1</b> evaluaciones de funciones y adicionalmente un bucle. La evaluación de <b> más a la derecha en la i-ésima llamada en <b>Q<sub>NC</sub></b> es la misma que la evaluación de <b>f</b> más a la izquierda de la (i+1)-ésima llamada. La figura siguiente muestra y representa la situación en el caso de cuatro subintervalos, para una regla de cinco puntos.
<center>
https://cdn.steemitimages.com/DQmXbhLPXfRoHMjTBDNRuafjC3YZF7P2VavviAep2xTr5wt/fig28.png
<sub>Representación de la evaluación de la función para <b>Q<sup>(4)</sup><sub>NC</sub>(5)</b>. Elaborado en Inskcape, por @abdulmath.</sub></center>

Para evitar redundancia de las evaluaciones de <b>f</b> y un bucle con llamadas a los valores de función repetidas veces, es mejor no aplicar <b>Q<sub>NC</sub></b> a cada uno de las <b>b</b> subintegrales. En su lugar, calculamos previamente todas las evaluaciones de la función que sean necesarias y las almacenamos en un vector de columna simple, es decir, ```fval(1:n*(m-1)+1)```. Así, podemos calcular la combinación lineal que define la regla compuesta como mostraremos a continuación.

En el ejemplo anterior de la regla compuesta de cinco puntos, es decir, <b>Q<sup>(4)</sup><sub>NC</sub>(5)</b>, las 17 evaluaciones de funciones requeridas se almacenan en ```fval(1:17)```. Si <b>w</b> es el vector de peso para <b>Q<sub>NC</sub>(5)</b>, entonces
<center>
https://cdn.steemitimages.com/DQmewJPo3ERP2xknsVTuXev8o1AEjnttCCBjsQ2XJrqNyLW/ec36.png</center>

A partir de esto, concluimos que <b>Q<sup>(n)</sup><sub>NC</sub>(m)</b> es una suma de <b>n</b> productos internos, cada uno de los cuales implica el vector de peso <b>w</b> de la regla subyacente y una parte del vector ```fval```. La siguiente función muestra lo que acabamos de decir:
<center>
https://cdn.steemitimages.com/DQmRukVEJRcKWw1GLrUMn7DK2MdGSSdrxCrKESnYyY5FZcj/ec37.png
<sub>Función la Regla Compuesta optimizada. Elaborado con GNU Octave, por @abdulmath.</sub></center>

<hr>
https://cdn.steemitimages.com/DQmaTz241KQheijV5qjopsqAzLW8ZpBqCmKmjpaixyGV4Wz/STEMESPANOL06.png
<hr>

<h3><div class="phishy">Error</div></h3>

Ahora, veamos como es el error cometido. Supongamos que <b>Q<sub>i</sub></b>2 es la estimación de <b>m</b> puntos de Newton-Cotes de la <b>i</b>-íesima subintegral. Si esta regla es exacta para polinomios de grado d, luego usando la ecuación (1) obtenemos la siguiente relación
<center>
https://cdn.steemitimages.com/DQmPypLCpvJgEqoDtj4gHJ93nCnotgTymeL5gqWX8hiLexr/ec38.png</center>
Por definición
<center>
https://cdn.steemitimages.com/DQmfBdAzHhxqD4Q7bhmjKFbmzcUfcqVfbJ7QzDTFkq4HWZf/ec39.png</center>
y
<center>
https://cdn.steemitimages.com/DQmcHaABKdrHrshPnMo7etEZPc2boa2kYfMxobADWyQFXWy/ec40.png</center>
Sin embrago, se puede demostrar que
<center>
https://cdn.steemitimages.com/DQmSSNiB3cGoPLNsh6EyUyPAMZPDnvNWnZn4ExrhrLQLTQp/ec41.png</center>
para algún valor de eta en <b>[a, b]</b> y así
<center>
https://cdn.steemitimages.com/DQmRLVAF2URv5t8sGTChYhvMhR9RyFyVTUF4rCPeKWpwNjq/ec42.png</center>
Si <b>|f<sup>(d+1)</sup>(z)|</b> es menor o igual a <b>M<sub>d+1</sub></b> para todo <b>x</b> en el intervalo <b>[a, b]</b>, entonces 
<center>
https://cdn.steemitimages.com/DQmbXDV3UhVK3M6qV4v1SRHa2eSgoQBtJVoydEg8cz2VKdb/ec43.png</center>

Si comparamos  con el error obtenido para la regla de Newton-Cotes (ver la ecuación (3) en <a href="https://steemit.com/steemstem/@abdulmath/integracion-numerica-con-gnu-octave-or-1era-parte">Integración Numérica con GNU Octave | 1era Parte</a>), vemos que el error en la regla compuesta es el error en la regla correspondiente simple dividido por <b>n<sup>d+1</sup></b>. Así, con un valor de <b>m</b> fijo, es posible ejercer el control del error eligiendo un valor de <b>n</b> suficientemente grande. Por ejemplo, supongamos que queremos aproximar la integral con una regla de Simpson compuesta uniformemente espaciada para que el error sea menor que una tolerancia prescrita. Si sabemos que la cuarta derivada de <b>f</b> está acotada por <b>M<sub>4</sub></b>, entonces elegimos <b>n</b> tal que
<center>
https://cdn.steemitimages.com/DQmZ43dBBpkQJXLxr2fcjj2RexR5nmntM6uKbXQwX79dgtB/ec44.png</center>
Para mantener el número de evaluaciones de la función lo más pequeño posible, <b>n</b> debe ser el número entero positivo más pequeño que satisfaga la siguiente relación
<center>
https://cdn.steemitimages.com/DQmPG7Mv1fqFAmaoavMj7hzdJPyvWoikmV7xKUzQSSjn2ry/ec45.png</center>
El siguiente script, muestra dos ejemplos donde se aplican lo visto para dos funciones simples
<center>
https://cdn.steemitimages.com/DQmYVGBRfnqsr4Jgh9t5iVwFhi61X2ZQsbTzpa97L2f2U9v/ec48.png
<sub>Script de aplicación para cálculo del error. Elaborado con GNU Octave, por @abdulmath.</sub></center>

Ahora veamos los gráficos obtenidos anteriormente.
<center>
https://cdn.steemitimages.com/DQmXi78chfrhkV38rY22uSydJrfnxX5Esn49p5u4fCjYiEv/NewtonCotes01.png
<sub>Gráfica del error de aproximación de la integral para la función <b>f(x) = sin(x)</b>. Elaborado con GNU Octave, por @abdulmath.</sub></center>
y
<center>
https://cdn.steemitimages.com/DQmaxTdur5AtyaAysnAfZeK28vCyfA6CXFKV9n8wq3MYsAM/NewtonCotes02.png
<sub>Gráfica del error de aproximación de la integral para la función <b>f(x) = sqrt(x)</b>. Elaborado con GNU Octave, por @abdulmath.</sub></center>

<hr>
https://cdn.steemitimages.com/DQmWXaTLF4uGH9x4QgPh29vKFUfyTGrzPaN2v4zytNiEEzC/SeparadorGMath33.png
<hr>

<h1><div class="phishy"></div>Adaptatividad</h1>

Las reglas compuestas uniformemente espaciadas que son exactas para polinomios de grado <b>d</b> son eficientes si <b>f<sup>(d+1)</sup></b> se comporta uniformemente en <b>[a, b]</b>. Sin embargo, si la magnitud de esta derivada varía ampliamente a lo largo del intervalo de integración, entonces el proceso de control de errores anteriormente puede resultar en una cantidad innecesaria de evaluaciones de la función. Esto se debe a que el valor de <b>n</b> está determinado por una cota <b>M<sub>d+1</sub></b> de la derivada a lo largo del intervalo. En regiones donde <b>f<sup>(d+1)</sup></b> sea pequeña en comparación con este valor, los subintervalos son mucho más pequeños de lo necesario. Los métodos de cuadratura adaptativa abordan este problema descubriendo dónde el integrando se comporta mal y disminuye el tamaño de los subintervalos en consecuencia.

<h3><div class="phishy">Un Proceso Adaptativo de Newton-Cotes</div></h3>

Para obtener una buena partición de <b>[a, b]</b>, debemos poder estimar el error. De esta forma, la partición puede ser refinada si el error no es lo suficientemente pequeño. Una idea es usar dos reglas de cuadratura diferentes. La diferencia entre los dos valores predichos de la integral podría tomarse como una medida de su inexactitud.

La forma de realizarla es similar al que desarrollamos para la aproximación lineal por tramos adaptativa (ver <a href="https://steemit.com/steemstem/@abdulmath/interpolacion-polinomial-a-trozos-usando-el-entorno-gnu-octave-or-1era-parte">Interpolación Polinomial a Trozos usando el entorno GNU Octave</a>). Para ver los detalles debemos desarrollar el método para estimar el error.

Fijemos <b>m</b> y sean
<center>
https://cdn.steemitimages.com/DQmPqu4911QrrzX6EmYzt84aHzG5PFUVGscgoAQk9htrw7R/ec49.png</center>
Por lo tanto, <b>A<sub>1</sub></b> es la estimación de regla de <b>m</b> puntos simple y <b>A<sub>2</sub></b> es la estimación de regla de <b>m</b> puntos en 2 intervalos. Si estas reglas son exactas para polinomios de grado <b>d</b>, entonces se puede demostrar que
<center>
https://cdn.steemitimages.com/DQmZCLx6H2i4qmzyhAHynnneXNSVRaWvezLXtjQwHjeLjMX/ec50.png</center>
Supongamos que 
<center>
https://cdn.steemitimages.com/DQmWP3WTCtm1poaBnj71zevXby6PzRsJnf3sMuYdArN3TSB/ec51.png</center>
Lo cual, es bastante razonable si <b>f<sup>(d+1)</sup></b> no cambia mucho en <b>[a, b]</b>. Por lo tanto, <b>I = A<sub>1</sub> + C</b> y  <b>I = A<sub>2</sub> + C/2<sub>d+1</sub></b> donde
<center>
https://cdn.steemitimages.com/DQmW59QHNthEgb3TcEHVWn5NpxsiXMKVCaeJeaTQBfTRbNC/ec52.png</center>
Al restar estas dos ecuaciones para <b>I</b> y resolver <b>C</b>, obtenemos
<center>
https://cdn.steemitimages.com/DQmet7xg9bubE6otqcLyzt1D7a3WpJiQ7J7pXQQV9FkYnGw/ec53.png</center>
y así
<center>
https://cdn.steemitimages.com/DQmevqiDpBZeD1ekBKhhhjetq66YJWCVJFTBmHPQRcuZD2B/ec54.png</center>
Por lo tanto, la discrepancia entre las dos estimaciones divididas por <b>2<sup>d+1</sup> - 1</b> proporciona una estimación razonable del error en <b>A<sub>2</sub></b>. Si nuestro objetivo es producir una estimación de <b>I</b> que tenga un error absoluto ```tol``` o  menor, entonces tenemos la siguiente función:
<center>
https://cdn.steemitimages.com/DQmVnL6NQUY8aKHY8MPcUHsCzUH3fwN2yNufdisE4xCAA6A/ec55.png
<sub>Función para calcular al integral de la función <b>f(x)</b> adaptada. Elaborado con GNU Octave, por @abdulmath.</sub></center>
Si la estimación heurística del error es mayor que ```tol```, se inician dos llamadas recursivas para obtener estimaciones
<center>
https://cdn.steemitimages.com/DQmWLyVx5FEjdqiGWRjcodwNAyCTC7ZkpwGa81ZKaLuV9UA/ec56.png</center>
que satisfacen
<center>
https://cdn.steemitimages.com/DQmf7no8UwydknN5x7CAtLLurgJSkMwW96ECQX4DF3P76Lo/ec57.png</center>
Configurando, <b>Q = Q<sub>L</sub> + Q<sub>R</sub></b>, vemos que
<center>
https://cdn.steemitimages.com/DQmagg8XcRoMhC59Vj8BRU9d6KC7AgnrJUFy5qF1RjjtzHW/ec58.png</center>
El siguiente script muestra como usar la función ```AdapQNC``` para varios valores de ```tol``` y <b>m</b>
<center>
https://cdn.steemitimages.com/DQmXsYzYdGeNC8jh3g2mME6bXrs28HHQjgTU4t74RUFWGyF/ec59.png
<sub>Script de applicación de ```AdapQNC```. Elaborado con GNU Octave, por @abdulmath.</sub></center>

Obteniendo los siguientes resultados, resumidos en la siguiente tabla

| |m = 3|m = 5|m-7|m = 9|
|---|---|---|---|---|
|tol = 0.01|(104,26)|(98,14)|(60,6)|(26,2)|
|tol = 0.001|(216,54)|(154,22)|(60,6)|(26,2)|
|tol = 0.0001|(376,94)|(210,30)|(140,14)|(130,10)|
|tol = 0.00001|(696,174)|(322,46)|(260,26)|(182,14)|

<hr>

<center>
https://cdn.steemitimages.com/DQmUJBiqZLfD8R8jp2C73YtxFZwNoTAE7zXRzyiUbigq74s/fig29.png</center>

<hr>
https://cdn.steemitimages.com/DQmdpxUb7HtnNdmxthWLKfUjnPA5sind9336Fgw5iy7pfv3/SeparadorGMath12.png
<hr>

Queridos amigos y lectores, espero hayan disfrutado y aprendido un poco más sobre la <b>Integración Numérica usando el entorno GNU Octave</b> donde pudimos aprender las ventajas de la integración numérica y como estimar el error cuando usamos este tipo de aproximaciones, también los invito a usar los script que les dejo y modificar las funciones dadas en los mismos y así poner en práctica todo lo que hemos aprendido hasta el momento. Estoy seguro que será de mucho apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

<br>Si desean consultar un poco más del tema pueden usar las siguientes referencias:
+ Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
+ Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
+ Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.
<hr>

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre,  GNU Octave, https://cdn.steemitimages.com/DQmYbufK9HG9LpAUVgEcFSNVmZG2irkjVy1duWbYqVyVtf4/LateX.png, GIMP e Inkscape.

<hr>
https://cdn.steemitimages.com/DQmaTz241KQheijV5qjopsqAzLW8ZpBqCmKmjpaixyGV4Wz/STEMESPANOL06.png
<hr>

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

<center>
https://cdn.steemitimages.com/DQmaSVacTwJ8v8uqJLMAKkNaLhisPAx7bi7KXVuzV1B3uQm/FinalGMath00.png
<sub>Imagen diseñada con GIMP y elaborada por @abdulmath.</sub></center>
</div>