This is an English version of my former [post](https://steemit.com/kr-math/@beoped/6gksol-1)

The purpose of this post is to show following vector-identities

![](https://steemitimages.com/DQmej5cKpxZicbbbzKY7x8Ld23zXDEqsNgF9zxRXMsExYjN/image.png)

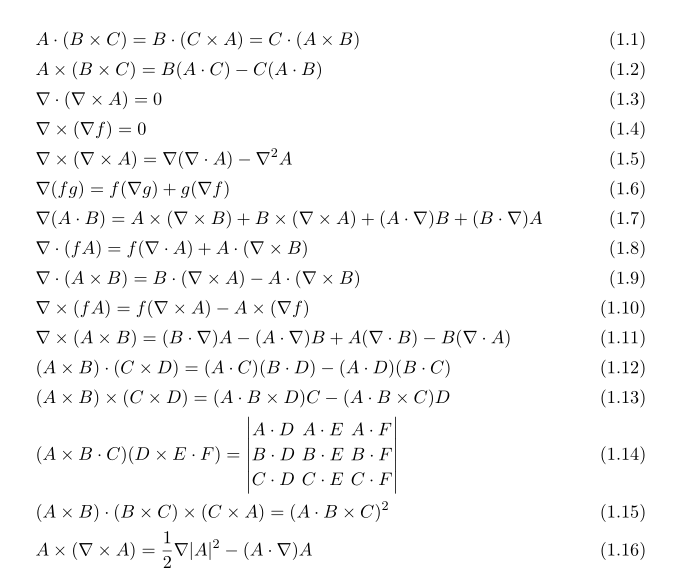
Here A,B stands for vector and f,g stands for scalar. Note that the inner product between two vectors are defined on arbitrary dimension, but in case of cross product it is ill-defined on some dimension. So we restrict this dimension as 3. 

These kinds of vector identities appeared in vector calculus, mathematical physics, mechanics, electrodynamics, fluid mechanics and many engineering  courses and textbook.  One can prove this with explicit computation via coordinate but here using some symbolic we will prove these equations. 

To do so we need some background, So at this post first we will cover **Einstein summation convention and representation of inner product and cross product**. And then after, at the second post, we will do explicit computation on these equations. 

Notation
-------------------

I'll skip some basic explanation on what is vector, but starting how to express vectors. 

![](https://steemitimages.com/DQmeXkGEkeszzDMizpjsV1zKAs2AvUyxEs29EkGurpZuGSb/image.png)

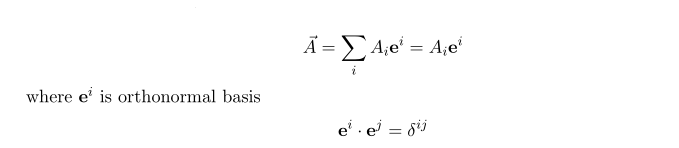
Here since we are assuming flat, the upper index and lower index does not give big difference. Einstein summation is nothing but a omit the sigma notation for summation as a convenience. Thus for the expression of repeated index, you should note that for your computation summation process for that indices  is required.  This notation is nothing to do with math but for saving some papers. 

Inner product and  kronecker delta 
--------------------------------------------
The inner product between two vectors is nothing but a function whose input is two vectors and output is a scalar. we can write them as follows
![](https://steemitimages.com/DQmSSEFQyKgMpbveQcDSNdht1GYsXu6LBYBUQkRoaiPtZ9a/image.png)

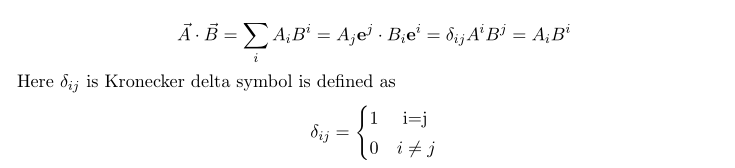
As from the definition, kronecker delta symbol is symmetric under the exchange of i and j

Cross product and Levi-civita symbol
-----------------------------------------------
The cross product between two vectors is nothing but a function whose input is two vectors and output is a vector, we can write them as follows

![](https://steemitimages.com/DQmTTZaQn9sd5tZcyCKHcbP91kYCt1KGBJGNoetSiC8fvhN/image.png)

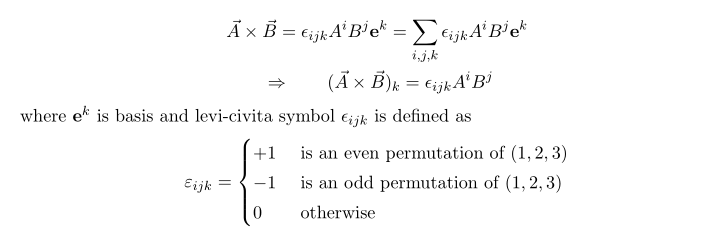
The other equivalent definition of Levi-civita symbols are

![](https://steemitimages.com/DQmPCoQ9QG2q5QRwJNNQu1wFb6K8qjjLgL9NSNgydV6jses/image.png)

Note you can see the three indices i,j,k are totally-anti symmetric. 

From this we can easily show some identities related with cross product 
![](https://steemitimages.com/DQmNPXAvLEqgosJ4FEA6LumAF5amgP3ZbtEhdewWYaTouCh/image.png)




About symmetry
------------------------------------------------------------------

First recall some definition. Note that 
 symmetric symbol S_[ij} and anti-symmetric symbol A_{ij} are defined by

![](https://steemitimages.com/DQma6i1rCSu17nEdvbMDHBwsN4gyQtfseRwHnBRHEn9n7wX/image.png)

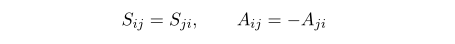
From this the contraction of symmetric symbol and anti-symmetric symbol always vanishes. 

![](https://steemitimages.com/DQmf11b9VNKzqypPdAWGsnhrzHeWonYYR2C1yETPM2R8iiN/image.png)


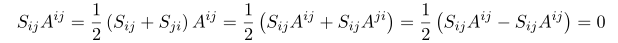
We are focusing on Levi-Civita symbol which has three index with totally anti-symmetric, thus we have 

![](https://steemitimages.com/DQmXJwjDvMfLFtswcprY8R6nxNLbGQwLjsuwtSk4eA1k7q4/image.png)

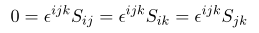
and this plays a important rule for derivation of vector calculus identities. 


Two product of Levi-civita symbol 
-----------------------------------------------------------

From the property of determinant 

![](https://steemitimages.com/DQmUyvhCt68RGTjWtNFZKhDHz1YonJSM5SuboBwYrUp9FVB/image.png)

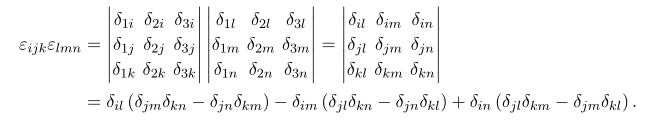
By plugging you can obtain 

![](https://steemitimages.com/DQmbdGF4kuXRABEVjkFkiMbY42S62kWqUkZeHFrq5BH92e5/image.png)


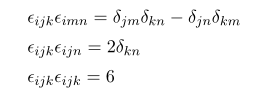
Generalization of n indices of Levi-civita symbol
-----------------------------------------------------------------------------------------------
One can define Levi-civita symbol with n index as follows

![](https://steemitimages.com/DQmcnmRPuJ4NpiTG2g2H8ejxVEh9a17N9WeyuRtyXny9W8h/image.png)

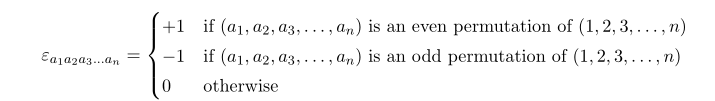
Again as the same way before we can equivalently express this in terms of determinant, thus the two product of them are nothing but 

![](https://steemitimages.com/DQmYytr9CVypS3rYkpzXgLy3y51BDXLFwDyM3cssv4PY3eQ/image.png)

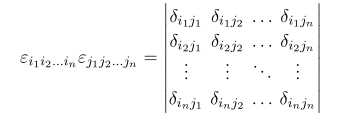
Thus
![](https://steemitimages.com/DQmWJab14p5Zm7AkhuUkwLYsonvhyCa77dPHSSzpEu14tFm/image.png)

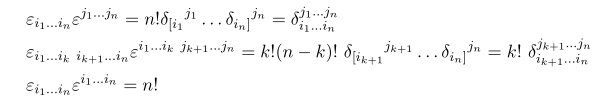
These kinds of things are important in the tensor computation. Note that tensor is some quantity which obeys some specific transformation rule. But this Levi-civita symbol is nothing but a numerical number thus not a tensor. In order to make it tensor we introduce so called "weight ", you can see this kinds of things in the computation of general relativity, 

Anyway, i will prove above 16 equation with these materials