<div class="text-justify">On this opportunity I want to give a special greeting to all friends and communities of steemit, especially to all those who support Spanish-language publications oriented to scientific and academic content. On this occasion I want to explain everything concerning the study and understanding of the derivative and the tangent line.
<p>
It is really with the settlement of the derivative that the true foundations of modern calculus are born, prior to the discovery of the derivative, the calculus studies focused on answering basically four fundamental problems: the tangent line problem, the velocity problem and the acceleration, the problem of maximums and minimums and the problem of the area.
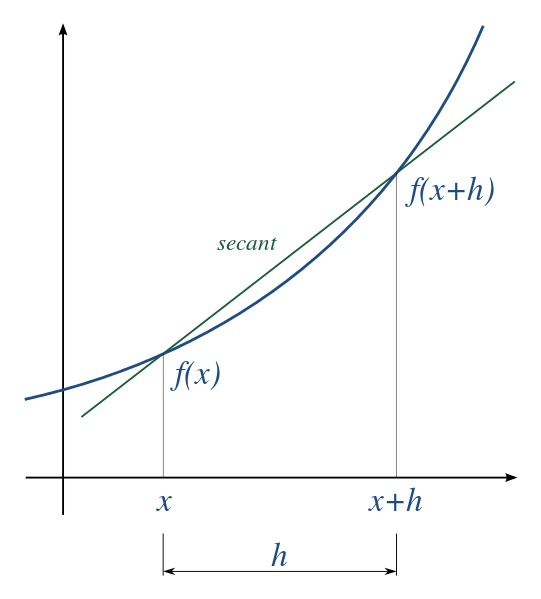
[Image source](https://commons.wikimedia.org/wiki/File:Derivative.svg)
***Note: the image has been copied from wikimedia commons, the author of the image is Olivier cleynen, who declares this image in the public domain.***
There were philosophers and mathematicians who worked to solve these four problems, arriving at the conclusion that everything had answers in approaching an arbitrary point to the tangential point by means of the limit theory (what we know today as derived from a function). However the most successful works were those of Isaac Newton and Gottfried Leibniz, which translate into the following definition:
***Definition of the tangent line with slope m***
<blockquote>
If f is defined in an open interval that contains c and there is a limit, it implies that:
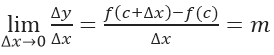
Then, the line that passes through (c, f (c)) and has a slope m is the line tangent to the graph of f at the point (c, f (c)).
</blockquote>
***Textual quotation: Calculation book. Volume I. Author: Larson and Hostetler. Section 2.1. Page: 97***
The way to find the tangent line with slope m at a given point by means of the limit theory, gives way to the most accepted definition that we now know of the derivative, and that is that when the derivative was discovered, an crucial point in the infinitesimal calculation, since with the limit used to define the slope of a line is also used to define one of the two fundamental operations of the calculation: the derivation. ***The derivative of f in x is given by:***

For this definition we must bear in mind that whenever the limit exists, the function is derivable, if the limit does not exist, the function is discontinuous and not derivable.

[Image source](https://commons.wikimedia.org/wiki/File:Derivative.svg)
***Note: the image has been copied from wikimedia commons, the author of the image is Olivier cleynen, who declares this image in the public domain.***

[Image source](https://commons.wikimedia.org/wiki/File:Dydx.jpg)
***Note: the image has been copied from wikimedia commons, the author of the image is Goldencako. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. Subject to waivers.***
### Example of derivative calculation of a function applying the derivative definition
<p>
***Calculate the derivative of***
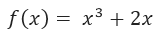
The first thing would be to propose the definition of the derivative:

In this case where the variable x is present, it is replaced by x + Δx and that c = x, this implies that:
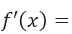 
Once replaced x by (x + Δx) and f (x) by  We have to solve the remarkable product 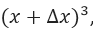 you have to solve the multiplications of 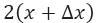 and  applying the distributive property, then we will remain as follows:

Performing the algebraic sum of the terms of the numerator, we would have the following:

It is convenient to extract common factor Δx in the numerator, in order to be able to simplify with the Δx of the denominator, which implies that:

The Δx of the numerator and denominator is canceled, and we would have the following expression:

If we make the limit of the function when Δx → 0, we have to replace Δx by zero, therefore:

With which we can conclude that the derivative of the function, that is, f '(x) is equal to:
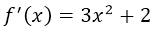
### Conclusions and lessons learned
1. The hard work of Leibniz and Newton to find the solution to the problems of the tangent line and the problem of acceleration and speed was conclusive to get to discover what we know today as derived from a function.
2. Mathematical work in the infinitesimal calculus did not end up proposing the derivative as a definition, but it evolved with demonstrations until a series of basic derivation rules were obtained, which make the work of deriving real functions much easier today. At the same time, this evolution allowed certain areas of engineering and science to find practical applications with the resolution of derivatives in terms of phenomena where the variables change with respect to each other.
3. In publications that I will upload later I will explain the mechanisms that facilitate the resolution of derivatives in a more explicit and easy way compared to those derived by definition, all this occurs when the basic rules of derivation are used, which are used with the intention of to minimize efforts and to understand more the processes to derive by tables that by definition.
4. In its own judgment, it is advisable that any person who starts in the study of derivatives, understand that the process of derivation is not a mechanized process, where through a series of formulas a series of steps are carried out to find the derivative of a function, that is, we must be aware that each time the derivative of a real function is solved, what is being achieved is the value of the slope of the line that is tangent to the function at a given point. In this way we will be very aware of what we are getting and not memorize steps and mechanize procedures.
### References consulted
- Calculation with analytical geometry. Author: Ron Larson and Robert P. Hostetler. 8th edition. Editorial Mc Graw Hill. Volume I. Mexico 2006.
- The calculation. Author: Louis Leithold. 7th edition. Editorial Oxford. Mexico 1998.
______________________________________________________________
***"For anyone who is passionate about mathematics, physics, chemistry, biology, education and engineering, I recommend the label of #steemstem, it is a community that values the intellectual and academic content of quality, always maintaining the originality of publications, so it is recommended to all those friends of steemit who wish to publish using this label not to commit plagiarism."***</div>

 hiveblocks
hiveblocks