이 문제를 다루기 위해서 필요한 Numpy 명령 몇가지 실습을 우선 해보도록 한다. 이 연습은 아나콘다 스파이더 편집기의 셸(Shell)에서 실행하도록 한다.
3개의 랜덤한 원소를 가지는 리스트를 2개를 생성하여 어레이화 하고 각 리스트의 첫 번째와 두 번째 값들이 0.0 보다 큰지 체크하여 XOR 데이터를 만들자. 둘 다 0.0보다 크든지 아니면 둘다 0.0 보다 작으면 False, 둘중에 하나가 양수고 나머지가 음수면 True가 된다.
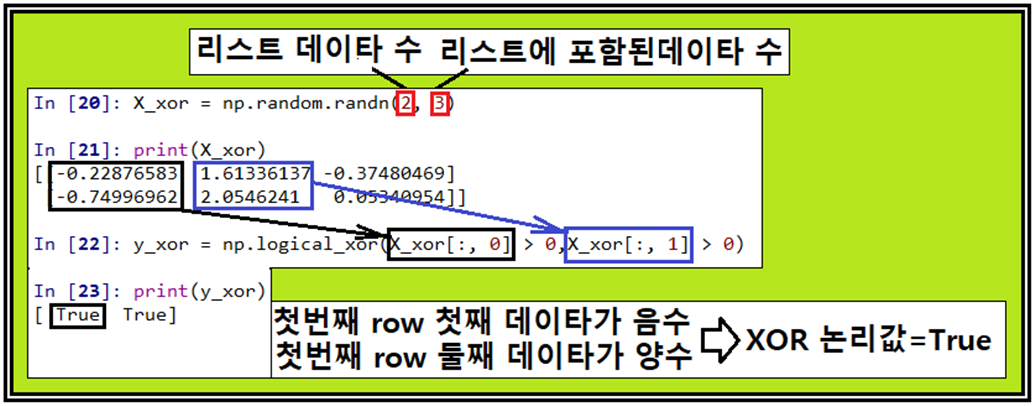
다음 예제에는 False 와 True 가 되는 데이터이다.

이 정도의 백그라운드 코딩 실력이 갖추어졌으면 다음과 같이 2개의 원소로 이루어진 200개의 리스트를 생성하여 어레이화 하여 스캐터 플롯을 해보자.

작도 결과를 살펴보면 True 데이터와 False 데이터가 서로 크로스한 형태로 분포되어 있음을 알 수 있다. 이 2종의 데이터를 대상으로 scikit-learn의 SVM기법을 적용하여 classification 작업을 해보자. 방법은 SVC 루틴을 부른 후 학습을 시켜 라벨 값 영역을 그래픽으로 작도해 보자.
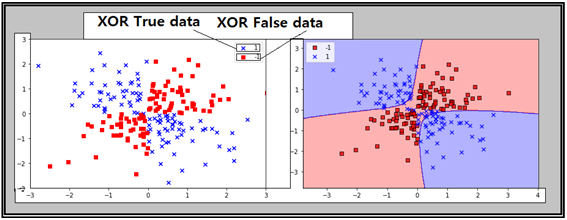
오른쪽 결과가 SVM 기법에 의해서 classification이 이루어진 결과이다. 퍼셉트론이나 Adaline 이나 Logistic regression 기법으로는 이런 결과를 뽑을 수는 없다는 점을 생각하면 왜 SVM 기법이 필요한지 쉽게 이해할 수 있을 것이다. 다음은 SVM 기법을 적용하는 SVC 루틴 사용 예이다. gamma 와 C 2개의 파라메터가 모종의 역할을 하고 있음을 알 수 있다.

SVM 기법에서 사용되는 gamma 파라메터는 Gaussian kernel 이란 명칭으로 다음과 같이 정의된다.
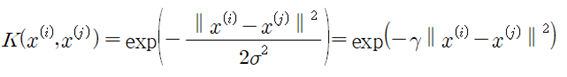
이 Gaussian kernel을 Radial Basis Function(RBF)이라고 하며 SVC 루틴에서 kernel 명으로 설정해야 한다. 커늘에 입력되는 2 데이터가 아예 동일하다면 K 값은 1.0 이 되며 완전히 이질적이면서 다르다면 gamma 값에 종속적이면서 0.0에 가까워지게 된다.
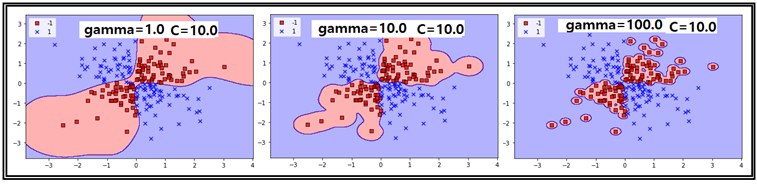
gamma의 파라메트릭 효과를 관찰해보기 위해서 C=10.0 조건으로 고정시킨 후 gamma=1.0, 10.0, 100.0 인 경우를 다음과 같이 작도해 보자. gamma 값이 커짐에 따라 False 데이터들이 아주 타이트하게 classification 됨을 알 수 있다.
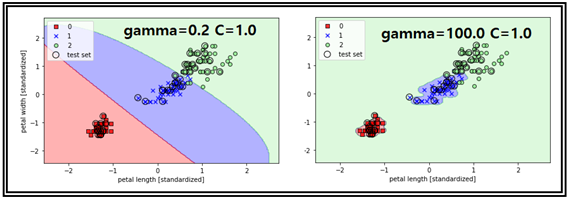
다음의 그래픽 처리 결과는 Iris flowers data set에 SVM 기법을 적용한 결과이다.
특히 gamma 값이 엄청 클 때에 라벨 값이 “0”이거나 “1”일 때에 decision boundary 경계가 엄청 타이트함을 알 수 있다. gamma 값이 SVM 기법 적용에 있어 아주 극단적인 처리 결과 예제를 살펴 보았다. 하지만 처음 접하는 데이터를 처리할 때에 일반적으로 높은 오차를 보일 가능성이 높다.
아래에 첨부된 코드는 랜덤하게 생성된 200개의 XOR 데이타 작도와 SVM 처리를 위한 코드이며 Iris flowers data를 사용하는 표준화 부분부터 이어져 오는 코드의 길이 문제로 그 부분은 생략하였다.
#ch02_data_read_1_2.py
from sklearn.svm import SVC
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
#setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.8,
c=colors[idx],
marker=markers[idx],
label=cl,
edgecolor='black')
if test_idx:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0],
X_test[:, 1],
c='',
edgecolor='black',
alpha=1.0,
linewidth=1,
marker='o',
s=100,
label='test set')
np.random.seed(1)
X_xor = np.random.randn(200, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0,
X_xor[:, 1] > 0)
y_xor = np.where(y_xor, 1, -1)
plt.scatter(X_xor[y_xor == 1, 0],
X_xor[y_xor == 1, 1],
c='b', marker='x',
label='1')
plt.scatter(X_xor[y_xor == -1, 0],
X_xor[y_xor == -1, 1],
c='r',
marker='s',
label='-1')
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend(loc='best')
plt.tight_layout()
plt.show()
svm = SVC(kernel='rbf', random_state=1, gamma=100.0, C=10.0)
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor,
classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show() hiveblocks
hiveblocks