자연과 우주를 대상으로 하는 물리학적 직관에 의해서 시작된 Boltzman의 통계역학이 1800년대 후반에 시작되어 그 영향이 1920년대 확률을 바탕으로 하는 양자물리학에 큰 영향을 끼쳤으리라 보이며 아울러 물리학 전반을 확률의 문제로 뒤바꿔 놓은 것이 사실일 것이다. 하지만 그보다 반세기를 넘어 훨씬 늦게 시작된 머신 러닝도 결국은 볼츠만의 확률분포에 기원한 Softmax 라든지 Fermi-Dirac 확률분포를 사용하는 Sigmoid 함수 사례에서처럼 그 여파가 현재에도 미치고 있는 듯하다. Boltzman의 통계역학을 차용했다고 보이는 Softmax에 대해서는 이미 논의가 되었으며 이번에는 Fermi-Dirac 확률분포를 차용했다고 보는 Sigmoid 함수에 대해서 알아보기로 한다.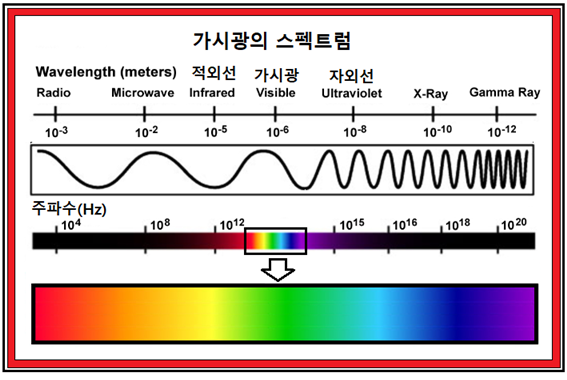

![noname01.png](https://cdn.steemitimages.com/DQmfHQR2uDgvfnaWQhJUgevu5RFKjRU2RaVAg8EbKna39Pi/noname01.png)

Rosenblatt에 의해 구체화된 머신 러닝을 위한 장치 즉 퍼셉트론에서 이미지를 인식하기 위하여 20X20 총 400개의 조도센서( photocell)를 사용하였다. 이 조도센서는 입사되는 빛의 밝아짐에 따라 저항 값이 감소하는 반도체로서 다시 말하면 빛의 밝기에 따라 전기전도(photoconductivity) 특성이 민감하게 변화하는 반도체이다. 이러한 특성으로 인해 빛을 검출하는 회로라든지 또는 빛에 의해서 밝아지거나 어두워지게 되면 회로를 스위칭하여 활성화 시키는데 사용이 가능하다.

아두이노 회로에 설치된 조도센서는 손가락으로 가릴 경우 40KΩ 이상의 높은 저항 값을 가지며 암실 정도의 어둠속에서는 MΩ 수준까지 저항 값이 커지는 반면에 대낮의 태양광하에서는 수십Ω 수준까지 저항 값이 떨어지기도 하는데 이러한 현상이 일어나는 물리적 배경을 살펴보자.

가시광선을 포함한 빛은 입자적인 측면뿐만 아니라 한편 파동적인 측면을 동시에 다 가지고 있어 스펙트럼을 분석해보면 색상별로 주파수를 가지고 있음을 알아볼 수 있다. 만약 조도센서에 특정 주파수 이상의 파장을 가지는 가시광이 입사하게 되면 반도체 물질에 의해 흡수되는 광량자(photon)들이  반도체 내부의 전자들을 여기(excitation) 시킨 후 바운드시켜 전기 전도밴드 (conduction band) 영역까지 점프시킬 수 있을 정도의 충분한 에너지를 주어야 한다. 전도영역까지 점프한 전자들은 가해진 전압에 따라 쉽게 움직일 수 있는 자유전자 상태가 되며 반도체 물질의 저항 값이 작아짐과 동시에 전기 전도성이 높아지게 된다.

물리학 관점에서 가장 간단한 원자 구조를 보여 주는 수소원자에 대해서 고려해 보자. 그림에서처럼 수소가 가진 1개의 전자는 이산적인 에너지 레벨상에 위치하게 된다. 하지만 수소뿐만 아니라 어떤 물질의 원자라 해도 원자 사이의 거리가 가까워질 정도로 촘촘히 결합하게 되면 이 에너지 레벨 사이의 폭도 아주 촘촘해진다. 원자핵에 가까운 부분에 밀집된 에너지 레벨군은 Valence Band(공유 결합 밴드)를 구성하고 반면에 핵으로부터 멀리 떨어져 영향이 거의 없는 영역에서는 전기 전도밴드를 구성하게 되며 그 사이에 전자가 머무를 수 없는 금지 영역이 설정된다.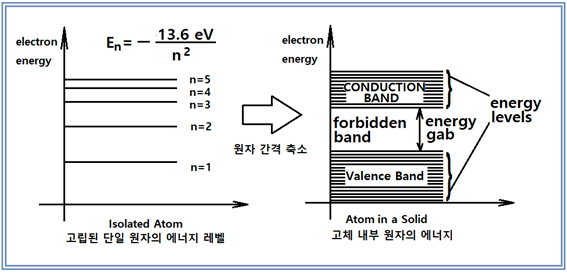

![noname02.png](https://cdn.steemitimages.com/DQmb1MxNoyrMprRr5z3GtTaqKbVCs6oRWogy9o8eEon9XQo/noname02.png)

이와 같이 빛에 의해 전기를 발생시키는 조도센서나 솔라셀을 만드는 반도체 재료에는 진성(Intrinsic)과 불순물형(Extrinsic, Imputities)의 두 가지 종류가 있다. 대표적인 반도체 재료로서 주기율표에서 원자 번호가 14번인 실리콘(Si)을 살펴보자.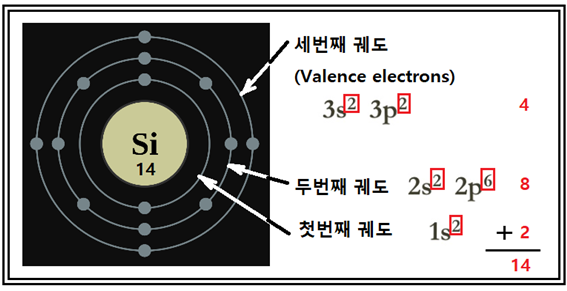 

![noname03.png](https://cdn.steemitimages.com/DQmUjGrm4A4wsmxANBmcSVEVSGLVc2Psjs77Gp7v5nWUQrk/noname03.png)

순수 실리콘은 14개의 전자를 가지는데 첫 번째 궤도(orbit)에 2개의 전자를 가진다. 이 2개의 전자는 파울리의 배타원리에 의해서 항상 스핀 방향이 반대되는 2개의 전자들만이 이 궤도를 채울 수 있다. 8개의 전자를 수용하는 두 번째는 2가지 종류의 궤도로 구성되며 마찬가지로 2종류의 궤도로 구성되는 세 번째 궤도는 물질 간의 공유결합(Covalent Bond)을 기준으로 최대 8개의 외곽전자가 들어갈 수 있는데 실리콘의 경우는 4개의 외곽전자를 가진다. 그림에서 박스 친 s 궤도들에서는 각각 2개의 전자만을 수용할 수 있는데 이는 파울리의 배타원리가 적용되는 영역이며 Fermi-Dirac 확률분포의 전제 조건이 된다. 원자들 간의 거리가 충분히 가까워지면 Valence Band 이든 Conduction Band 이든 에너지 레벨들 사이의 간격이 촘촘해지며 각 레벨에는 스핀이 서로 반대 방향인 2개의 전자가 들어가든지 아니면 1개의 전자가 들어갈 수 있게 된다.

고체 상태의 순수 실리콘은 인접하는 4개의 실리콘들로부터 각각 1개씩의 외곽 전자를 제공받아 자신의 4개 전자를 합하여 총 외곽 전자수 8개를 채우는 공유결합(Covalent Bond)을 한다. 하지만 순수 실리콘의 전기 전도도는 Conduction Band 에 전자들이 없는 상태이므로 그다지 좋지 않은 편이다.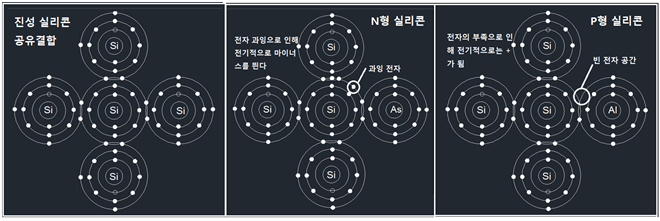 

![noname04.png](https://cdn.steemitimages.com/DQmf62VrM5DJoAjefyxh5VXCY7roMQCDNg6SLR6Er8G6yjw/noname04.png)

순수 실리콘 공유결합 구조에 +5가의 물질 즉 최외곽 전자가 5개인 물질(As:비소, Sb:안티몬 P:인)을 소량 불순물로 섞으면 그림에 표시된 것 같이 전도밴드(Conduction Band)에 위치하는 과잉전자가 생성되어 N형(Negative) 반도체 재료가 된다. 전압을 걸어주면 과잉 전자가 전압 반대 방향으로 쉽게 흐르게 된다. 

반대로 +3가의 물질(Al:알루미늄, In:인듐) 즉 최외곽 전자가 3개인 물질을 소량 불순물로 섞으면 그림에 표시된 것 같이 전도밴드(Conduction Band)에 위치하는 빈 전자공간이 생성되어 P형(Positive) 반도체 재료가 되며 전압을 걸어주면 과잉 전자가 전압 반대 방향으로 쉽게 흘러 들어오게 된다. P형과 N형을 조합하면 다이오드가 되며 threshold 이상의 정방향 전압 0.5V 이상을 걸어주게 되면 전류가 잘 흐르며 역방향 전압 하에서는 전류가 흐르지 않게 된다. 

전기 전도도 관점에서 물질은 즉 절연체, 반도체  및 전도체 3가지 종류로 나눌 수 있는데 에너지 밴드 이론으로 간단히 설명해 보자. 절연체는 Valence Band와 Conduction Band  사이의 에너지 갭이 대단히 커서 전자가 점프하기 힘든 물질인 반면에 반도체는 에너지 갭이 그다지 크지 않으며 중간에 Fermi level 이 있다. 도체의 경우는 두 영역이 겹쳐지는 현상이 일어나며 전자가 쉽게 옮겨갈 수 있을 정도이다.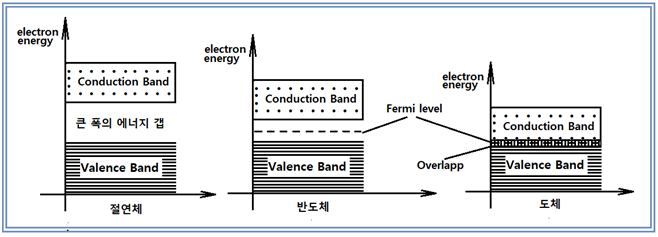 

![noname05.png](https://cdn.steemitimages.com/DQmTztXHPfBtnPYs1w1qjK4AoCrc3eqA8KySzpyp1vKPnZ8/noname05.png)

반도체 재료에 있어서 Fermi (energy) level은 전자가 Conduction Band 로 점프할 것인지 아니면 Valence Band로 갈 것인지 결정되는 확률 50% 지점을 나타낸다. Fermi-Dirac 확률분포식을 살펴보자.

E는 전자의 에너지 레벨이며 Ef는 Fermi 에너지 레벨로서 물질 별로 고유한 상수인 듯하다. 
k는 볼츠만 상수이며 T는 Kelvin의 절대온도이다. 

⓵ 만약 전자의 에너지 E 와 Fermi 레벨 Ef가 일치하면 확률 p(E)의 값은 0.5가 된다. 
⓶ E＞Ef 이면서 kT→0, p(E)→0
⓷ E＜Ef 이면서 kT→0, p(E)→1

이 세가지 경우를 포함한 확률 분포를 그래프로 표현해 보자. 아래의 그림을 왼쪽으로 90도 돌려서 보는 것이 이해에 도움이 될 것이다.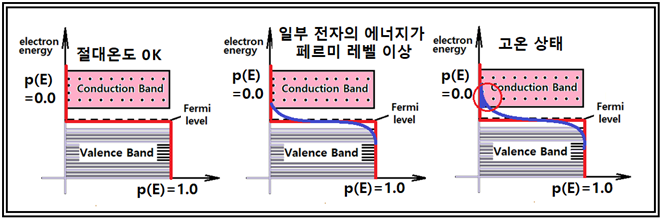

![noname06.png](https://cdn.steemitimages.com/DQmQvgpihJH52zGsbLPzvvBWe8wzZK7CzTQYuhZTTd3hGjN/noname06.png)

절대 온도 0 K인 첫번째 그림에서 E＞Ef 가 되는 조건하에 서 확률 p(E) 의 값이 0이라는 것은 Conduction  Band에 전자가 있을 확률이 전혀 없다는 의미이며 에너지 레벨 E가 페르미 레벨 보다 작으면 p(E)=1 이므로 모든 전자가 Valence Band 영역에 있다는 뜻이다.

페르미 레벨 이상에서 일부 전자가 있을 경우에는 p(E) 가 0 이상이 되는 부분이 조금 나타난다. 아예 온도가 많이 상승할 경우에는 전자들이 Conduction Band 에 위치하게 되며 전기 전도도가 좋아져 전류를 흘릴 수 있게 된다.

머신 러닝에서 Sigmoid 함수를 사용할 때에 확률이 0.0 인 경우와 1.0인 두 경우는 학습 단계에서 보기 좋게 “0”과 “1”로 각각 라벨 값을 부여할 수 있는 대상이 될 수 있을 것이다.  특히 Binary Classification 문제에서는 Softmax 사용도 가능하지만 Sigmoid 함수도 사용이 가능하므로 이미 Softmax를 적용했던 벤치마킹 문제에서 어느 정도 확률 값 계산에 차이가 있는지 비교를 위해 알아 볼 필요도 있는듯하다.

여기까지의 내용이 고체물리학(Solid State Physics) 분야에서 전자의 확률분포를 예측하는 Sigmoid 함수가 사용되는 원조 사례이다. 이런 물리학적인 내용이 과연 머신 러닝에 어떤 영향을 미칠지는 정확히 알 수 없지만 그래도 볼츠만 분포 확률에서 입자의 위치와 운동량이 MNIST 수식 숫자인식 문제에서 픽셀의 위치와 랜덤한 픽셀 값을 사용하여 뛰어난 인식률을 보여주는 Softmax 명령을 생각해 보면 항상 많은 가능성이 열려 있다고 볼 수 있을 것이다.