Hi there. This math post features some trigonometric identities (on right angle triangles) with math proofs. Math text are displayed as images through the use of QuickLaTeX.com. <center><img src="http://mirshahi.wikispaces.com/file/view/Right-Angled%20Triangle01.jpg/449483622/Right-Angled%20Triangle01.jpg" /></center> <center><a href="http://mirshahi.wikispaces.com/file/view/Right-Angled%20Triangle01.jpg/449483622/Right-Angled%20Triangle01.jpg">Featured Image Source</a></center> ### Review Of SOH CAH TOA & Reciprocal Trigonometric Functions --- Given an angle http://quicklatex.com/cache3/5f/ql_0ae11b7baabd364c4b2dac02c268bf5f_l3.png (theta) the trigonometric functions represent ratios of the side lengths of a right angle triangle. To save space, refer to the summary image below. (a = adjacent side length, o = opposite side length, h = hypotenuse length) <center><img src="https://study.com/cimages/multimages/16/sohcahtoa-triangle.jpg" /></center> <center><a href="https://study.com/cimages/multimages/16/sohcahtoa-triangle.jpg">Image Source</a></center> Note that when it comes to fractions, the denominator (bottom of a fraction) cannot be zero. Furthermore, angles which would make the denominator zero are not permitted. These trigonometric functions can be used in the xy coordinate system as shown in the image below. The angle is theta, the adjacent side to theta is `x`, the opposite side to theta is `y` and the hypotenuse is the radius. A unit circle of http://quicklatex.com/cache3/16/ql_38ae60eeec1d6e088db0d682dcfbae16_l3.png (where r = 1) is assumed. <center><img src="http://intmstat.com/analytic-trigonometry/Image477.gif" /></center> <center><a href="http://intmstat.com/analytic-trigonometry/Image477.gif">Image Source</a></center> The six trigonometric functions now become: <center>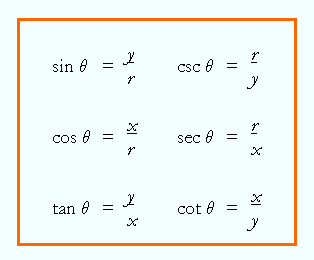</center> Screenshot Image From http://www.themathpage.com/aTrig/unit-circle.htm The bottom part of the fraction cannot be zero. ### A Few Trigonometric Identities With Proofs --- Here are a few trigonometric identities with proofs. It is assumed that the angle theta is from 0 to 360 inclusive. **Example One** <center>http://quicklatex.com/cache3/6a/ql_d4061bd9dcdeb4891a27100a7b7c4d6a_l3.png</center> The cotangent of an angle is 1 divided by the tangent of the same angle. With this in mind, the left side of the equation can equal one as follows: <center>http://quicklatex.com/cache3/e6/ql_559f88aed4d57e15630bd2fe94bc9de6_l3.png</center> An alternate way is using http://quicklatex.com/cache3/e8/ql_1764a8f1f6d12765c651cac00054a3e8_l3.png . Proofs of http://quicklatex.com/cache3/b1/ql_836a8a34ff054e35b3be0d1b511194b1_l3.png are done similarly. **Example Two** <center>http://quicklatex.com/cache3/f7/ql_566fd40936f6d5a9b2048efcd51feef7_l3.png</center> To start, we use the fact that http://quicklatex.com/cache3/8d/ql_c0287de2090465b192b50c36fe6a388d_l3.png and http://quicklatex.com/cache3/51/ql_da3dc91b366aba5abe818364c7543151_l3.png. The left side of the above equation becomes: <center>http://quicklatex.com/cache3/fc/ql_2ae1531212d63afcc91bafd04c7efafc_l3.png</center> What completes this proof is knowing that the top of the fraction is actually the equation of the circle. That is, http://quicklatex.com/cache3/b1/ql_ad5c730589ec133a78ac6e79b57fbcb1_l3.png where `r` is the radius of a circle. Using this idea, will turn the fraction into 1. <center>http://quicklatex.com/cache3/32/ql_3d248b683fded70f0fbfcb78beece432_l3.png</center> **Example Three** <center>http://quicklatex.com/cache3/be/ql_d8e71c576ac92da5dfa19abbd6cb6abe_l3.png</center> The tangent of an angle is http://quicklatex.com/cache3/00/ql_f4f732592f30243430cd233864588000_l3.png. This fraction would be squared and a common denominator needs to be determined. <center>http://quicklatex.com/cache3/a7/ql_c60b7fa43187e8e14705fbd3ac5bbea7_l3.png</center> Notice how the top of the fraction is the equation of the circle. This fact is used again along with exponent rules. The resulting ratio is the square of the secant of the angle. <center>http://quicklatex.com/cache3/f1/ql_e894d10a96f0b6d63b085b6080adcbf1_l3.png</center> **Example Four** <center>http://quicklatex.com/cache3/7b/ql_905d8fc84bd6457ba7d822b4e7a5e97b_l3.png</center> The cotangent of an angle is http://quicklatex.com/cache3/38/ql_438fd8935033e97c2754155d0b779038_l3.png With a substitution and algebra, once can obtain the right side of the above equation. <center>http://quicklatex.com/cache3/41/ql_78314249057ac4dcc49214653e067441_l3.png</center> ### References --- http://www.sosmath.com/trig/Trig5/trig5/trig5.html Functions 11 by Nelson Thomson
| author | dkmathstats |
|---|---|
| permlink | a-few-trigonometric-identities |
| category | math |
| json_metadata | {"tags":["math","mathematics","algebra","steemstem","steemiteducation"],"image":["http://mirshahi.wikispaces.com/file/view/Right-Angled%20Triangle01.jpg/449483622/Right-Angled%20Triangle01.jpg","http://quicklatex.com/cache3/5f/ql_0ae11b7baabd364c4b2dac02c268bf5f_l3.png","https://study.com/cimages/multimages/16/sohcahtoa-triangle.jpg","http://quicklatex.com/cache3/16/ql_38ae60eeec1d6e088db0d682dcfbae16_l3.png","http://intmstat.com/analytic-trigonometry/Image477.gif","https://steemitimages.com/DQmZk6aj1Fjiyb4BNHwQ5QcUeA5wDxyvz3QSETtXJPicHo3/mathpage_circleTrig.png","http://quicklatex.com/cache3/6a/ql_d4061bd9dcdeb4891a27100a7b7c4d6a_l3.png","http://quicklatex.com/cache3/e6/ql_559f88aed4d57e15630bd2fe94bc9de6_l3.png","http://quicklatex.com/cache3/e8/ql_1764a8f1f6d12765c651cac00054a3e8_l3.png","http://quicklatex.com/cache3/b1/ql_836a8a34ff054e35b3be0d1b511194b1_l3.png","http://quicklatex.com/cache3/f7/ql_566fd40936f6d5a9b2048efcd51feef7_l3.png","http://quicklatex.com/cache3/8d/ql_c0287de2090465b192b50c36fe6a388d_l3.png","http://quicklatex.com/cache3/51/ql_da3dc91b366aba5abe818364c7543151_l3.png","http://quicklatex.com/cache3/fc/ql_2ae1531212d63afcc91bafd04c7efafc_l3.png","http://quicklatex.com/cache3/b1/ql_ad5c730589ec133a78ac6e79b57fbcb1_l3.png","http://quicklatex.com/cache3/32/ql_3d248b683fded70f0fbfcb78beece432_l3.png","http://quicklatex.com/cache3/be/ql_d8e71c576ac92da5dfa19abbd6cb6abe_l3.png","http://quicklatex.com/cache3/00/ql_f4f732592f30243430cd233864588000_l3.png","http://quicklatex.com/cache3/a7/ql_c60b7fa43187e8e14705fbd3ac5bbea7_l3.png","http://quicklatex.com/cache3/f1/ql_e894d10a96f0b6d63b085b6080adcbf1_l3.png","http://quicklatex.com/cache3/7b/ql_905d8fc84bd6457ba7d822b4e7a5e97b_l3.png","http://quicklatex.com/cache3/38/ql_438fd8935033e97c2754155d0b779038_l3.png","http://quicklatex.com/cache3/41/ql_78314249057ac4dcc49214653e067441_l3.png"],"links":["http://mirshahi.wikispaces.com/file/view/Right-Angled%20Triangle01.jpg/449483622/Right-Angled%20Triangle01.jpg","https://study.com/cimages/multimages/16/sohcahtoa-triangle.jpg","http://intmstat.com/analytic-trigonometry/Image477.gif","http://www.themathpage.com/aTrig/unit-circle.htm","http://www.sosmath.com/trig/Trig5/trig5/trig5.html"],"app":"steemit/0.1","format":"markdown"} |
| created | 2018-01-20 01:10:12 |
| last_update | 2018-01-20 03:42:36 |
| depth | 0 |
| children | 3 |
| last_payout | 2018-01-27 01:10:12 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 17.484 HBD |
| curator_payout_value | 5.390 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 4,784 |
| author_reputation | 153,467,196,096,762 |
| root_title | "A Few Trigonometric Identities" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 30,748,213 |
| net_rshares | 2,069,011,844,616 |
| author_curate_reward | "" |
| voter | weight | wgt% | rshares | pct | time |
|---|---|---|---|---|---|
| pharesim | 0 | 88,908,240,521 | 0.02% | ||
| lafona-miner | 0 | 162,431,915,323 | 2.5% | ||
| hr1 | 0 | 50,229,247,242 | 0.02% | ||
| kushed | 0 | 4,878,700,200 | 2% | ||
| mrs.agsexplorer | 0 | 8,597,589,826 | 2% | ||
| justtryme90 | 0 | 259,744,221,166 | 10% | ||
| anwenbaumeister | 0 | 38,557,951,631 | 2% | ||
| roelandp | 0 | 86,656,974,043 | 1% | ||
| timsaid | 0 | 4,969,962,926 | 1% | ||
| velourex | 0 | 3,226,909,343 | 2% | ||
| cristi | 0 | 73,697,141,384 | 20% | ||
| lemouth | 0 | 17,140,870,378 | 5% | ||
| rjbauer85 | 0 | 157,941,436 | 5% | ||
| anarchyhasnogods | 0 | 13,716,614,281 | 5% | ||
| lamouthe | 0 | 982,437,612 | 5% | ||
| curie | 0 | 97,535,436,508 | 2% | ||
| hendrikdegrote | 0 | 1,032,054,203,003 | 2.4% | ||
| steemstem | 0 | 54,692,130,792 | 5% | ||
| foundation | 0 | 434,700,973 | 5% | ||
| the-devil | 0 | 1,067,866,315 | 5% | ||
| thevenusproject | 0 | 2,656,697,012 | 5% | ||
| dna-replication | 0 | 2,498,731,924 | 10% | ||
| jamhuery | 0 | 1,689,642,793 | 5% | ||
| mobbs | 0 | 5,839,439,227 | 2.5% | ||
| kryzsec | 0 | 951,151,867 | 5% | ||
| dber | 0 | 3,719,099,779 | 5% | ||
| kerriknox | 0 | 20,008,216,433 | 5% | ||
| alexander.alexis | 0 | 123,749,238 | 0.5% | ||
| mystifact | 0 | 741,300,112 | 5% | ||
| nitesh9 | 0 | 1,193,056,237 | 5% | ||
| fancybrothers | 0 | 764,646,022 | 3.5% | ||
| himal | 0 | 256,840,881 | 5% | ||
| ovij | 0 | 656,809,680 | 5% | ||
| azirgraff | 0 | 989,550,159 | 1% | ||
| mountainwashere | 0 | 1,177,287,196 | 5% | ||
| somethingburger | 0 | 5,322,023,214 | 100% | ||
| kingswisdom | 0 | 312,627,302 | 5% | ||
| fakhrizal | 0 | 3,555,759,075 | 100% | ||
| tormiwah | 0 | 440,442,400 | 3% | ||
| buildrobotics | 0 | 0 | 100% | ||
| alketcecaj | 0 | 0 | 33% | ||
| fabio2614 | 0 | 2,048,957,430 | 100% | ||
| carloserp-2000 | 0 | 652,279,187 | 5% | ||
| rachelsmantra | 0 | 193,103,174 | 5% | ||
| alistinaeva | 0 | 68,330,185 | 100% | ||
| annakoro | 0 | 218,925,306 | 100% | ||
| gra | 0 | 1,672,975,037 | 5% | ||
| kedi | 0 | 913,334,393 | 3.5% | ||
| ongoingwow | 0 | 152,698,720 | 4% | ||
| kenadis | 0 | 1,018,807,378 | 5% | ||
| amavi | 0 | 710,765,646 | 1% | ||
| geekpowered | 0 | 2,085,255,599 | 1% | ||
| gentleshaid | 0 | 1,222,416,306 | 5% | ||
| sco | 0 | 270,655,844 | 1% | ||
| datascience | 0 | 3,238,457,396 | 17% | ||
| sorryopozd | 0 | 52,874,406 | 100% | ||
| sadabi | 0 | 483,026,200 | 100% | ||
| joseferrer | 0 | 1,319,350,757 | 100% | ||
| hadji | 0 | 111,506,198 | 5% | ||
| pencentre | 0 | 0 | 100% |
excellent explanation friend already you vote, greetings
| author | joseferrer |
|---|---|
| permlink | re-dkmathstats-a-few-trigonometric-identities-20180120t125026662z |
| category | math |
| json_metadata | {"tags":["math"],"app":"steemit/0.1"} |
| created | 2018-01-20 12:50:33 |
| last_update | 2018-01-20 12:50:33 |
| depth | 1 |
| children | 0 |
| last_payout | 2018-01-27 12:50:33 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 56 |
| author_reputation | -56,563,599,716 |
| root_title | "A Few Trigonometric Identities" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 30,856,127 |
| net_rshares | 0 |
fyi. Your brackets would look better if you put left/right markers on them in the latex: {\left( \frac{x}{y} \right)}^2| author | peeterjoot |
|---|---|
| permlink | re-dkmathstats-a-few-trigonometric-identities-20180120t033107717z |
| category | math |
| json_metadata | {"tags":["math"],"app":"steemit/0.1"} |
| created | 2018-01-20 03:31:06 |
| last_update | 2018-01-20 03:31:06 |
| depth | 1 |
| children | 1 |
| last_payout | 2018-01-27 03:31:06 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 120 |
| author_reputation | 4,108,216,103 |
| root_title | "A Few Trigonometric Identities" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 30,770,549 |
| net_rshares | 0 |
Okay. Fixed. Thank you for the tip.
| author | dkmathstats |
|---|---|
| permlink | re-peeterjoot-re-dkmathstats-a-few-trigonometric-identities-20180120t034309999z |
| category | math |
| json_metadata | {"tags":["math"],"app":"steemit/0.1"} |
| created | 2018-01-20 03:43:09 |
| last_update | 2018-01-20 03:43:09 |
| depth | 2 |
| children | 0 |
| last_payout | 2018-01-27 03:43:09 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 35 |
| author_reputation | 153,467,196,096,762 |
| root_title | "A Few Trigonometric Identities" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 30,772,379 |
| net_rshares | 0 |
 hiveblocks
hiveblocks