Let us consider a medium that is source free, that is, there are no charges and no current and the region is unbound, that is no boundary conditions to be applied. Now the question that comes to the mind is what form will the electrical and magnetic field take in this medium? . At this point we ask the question how will the electric and magnetic field be formed in such a medium (we said no source). The question now will be what will be the relationship between the electric and magnetic field in this unbound surface medium. So we will investigate the relationship between electric and magnetic field in this unbound source free medium. Let us also assume the solution we get from this equation will be simple and consistent with maxwell’s equations, so we look for solutions consistent with maxwell’s equations. What we mean by this is, if we look at the simplest solution which is consistent with the constraint, if we take the simplest example that if a function was known at one point, then the simplest solution will be a function constant passing through that point. If we know the function value at two point, then it will be a linear function passing through the two point and so on.
Of course we have two points and we have infinite functions which can pass through these point, however we said earlier that we would accept the simplest solution which will be linear solution consistent with the value of the function at these two point. This is the same thing we going to do for solution to the maxwell’s equations. We will take the simplest solution that is consistent with the maxwell’s equation, if it is not, we increase the complexity of the solution until it is complex and consistent with maxwell’s equations. Let us consider an unbound, isotropic, homogeneous region (no sources).
Unbound: No boundary condition to be applied.
Isotropic: That is permittivity and permeability are scalar quantities.
Homogeneous: That is, the medium permittivity and permeability are not functions of space and time.
charge density ρ = 0
current density J = 0
So we can write the maxwell’s equation as
<br>

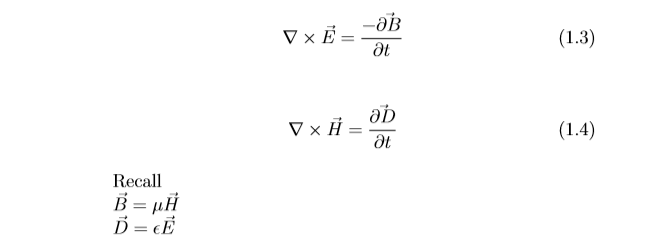
<br>
ε and µ are scalar quantities. However the µ and epsilon are in unbound medium which is similar to free space. The permittivity and permeability for free space are denoted by µ(0) and epsilon(0). Let us consider a dielectric medium which is unbound but not necessarily free space. We have that the medium have µ and epsilon but no boundary to this medium. What will be the relationship between electric and magnetic field in this medium?
if µ = µ0 and ε=ε(0) we would get a solution corresponding to free space Substituting B and D in equation 1.3 and 1.4
<br>
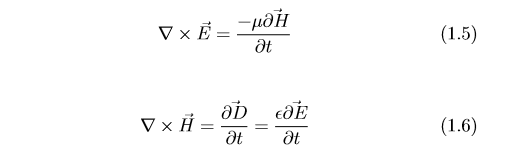
<br>
In electrical engineering, we solve the problem for periodic signals and periodic signal can be decomposed to its fourier series. If we find out the behavior of the system for a sinusoidal signal, we can always find the response of the system for periodic signals. So let us assume without loosing generality that we investigate the problem here for the time harmonic fields. Let us assume that both electric field and magnetic field are both function of time. That is E and H are time varying function and are sinusoidal function of time.
where ω = the angular frequency. So far our earlier assumption when we differentiate a time varying function of e^(jωt)
<br>

<br>
The equation for unbound, homogeneous medium derived from general maxwell’s equation. Looking at the last two equation , the space derivative of the electric field is relative to time derivative of magnetic field, so essentially now we are looking for the solution of these four equations. If we look at ∇× E = −jωµH and ∇×H = jωµ E, ∇×E is dealing with partial derivative of the electric field and is related to the time derivative −jωµH of the magnetic field. If we recall this equation is similar to that of TL(Transmission Lines). For the transmission line equation replacing electric field by voltage and magnetic field by current, then TL we had derive the voltage equal to −jωLI. So µ which is permeability it has unit H/m, electric field E has unit v/m, H is A/m. So if we take the per meter out the E will be volts, µ will be H and it will be A. So ∇×E = −jωµH is identical with the equation in TL. Exactly similar thing happens in ∇× H = jωµE. That is the space derivation of electric current is related to jωE which is like capacitance and current. ∇× E = −jωµH and ∇× H = jωµE, are generalize form of these equation in TL. So here we are having a three dimensional space. Also here we are having electric and magnetic field which are not scalar as that TL.
So we have these vector quantities ∇×E = −jωµH, which have a derivative in 3D space denoted by the ∇operator. So TL case which we have discussed in a special case of this generalize 3D case. Also as we have found out when analyzing TL. These solution are coupled equation, so that the electric field E is related to the magnetic field and the magnetic field is related to the electric field. So if we want a solution for both electric and magnetic field, we have to decoupled the two equations ∇× E = −jωµH and ∇×H = jωµE. We also noted that both H and E are vectors quantities, that we define the space derivative, we ask what is meant by space derivative since H and E are vectors quantities, in terms of simple space function the derivatives was ∂/∂x, ∂/∂y, ∂/∂z. However we are talking about space derivatives in 3D space, we can operate space derivative ∇×E = −jωµH and ∇×H = jωµE which would like divergence operator or like curl operator on ∇×E and ∇×H. So either we find the divergence of the equation or we find the curl of the equation and this are the two ways to find the space derivatives of the equation. Divergence of∇×E is identically zero. So that∇·(−jωµH) = 0 from ∇×E = −jωµH, take derivatives of both sides ∇·(∇×E) = ∇·(−jωµH) or ∇·(−jωµH) = 0 similar to µ∇·H = 0. We would have the same thing happen if we carry out divergence on ∇× H = jωµE on both side, the equation reduce to epsilon·∇·E = 0 which we had already. So divergence as a space derivatives carried out on the coupled equation ∇×E = −jωµH and∇×H = jωµE did not give us any other different expression we have not had before. So we try to take curl of both side of the equation which is another form of space derivatives.
It will be observed that the coupled equation for voltage and current in a transmission is analogous to the space equation for the electromagnetic wave. Essential equation (1.7) and (1.8) are generalized from these equations.
No new equation will be formed when taking the divergence, so let us take curl of equation (1.9)
<br>
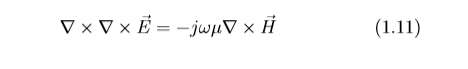

<br>
Equation (1.14) govern the electric field while Equation (1.18) govern the magnetic field, and they are similar. Each of these equations consist of three equations, i.e three components of E in cartesian co-ordinate (Ex,Ey,Ey) that satisfies the equation and that of H (Hx,Hy,Hy) satisfies the equation.
The generalised form for wave equation gotten in transmission line is
<br>
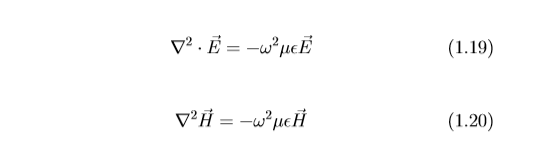
<br>
So what we want to get is the solution to the set of equations that solve maxwell’s equations.
We want to proceed from the simplest possible solutions and ask if the solution is consistent with maxwell’s equations.
<br>
### Case 1 :
Let say the electrical field ( E ) is uniform in the three dimensional space,
<br>
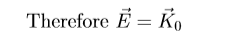
<br>
we do not always put e^(jωt) as we assume it is implicit in all the solutions that we are defining. So when we require an instantaneous value we always multiply by e^(jωt). For E =K(0) to be consistent with maxwell’s equation it must satisfy the equations which we have derive. So we can substitute E into equation (1.11).
<br>
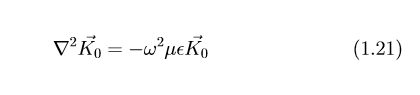
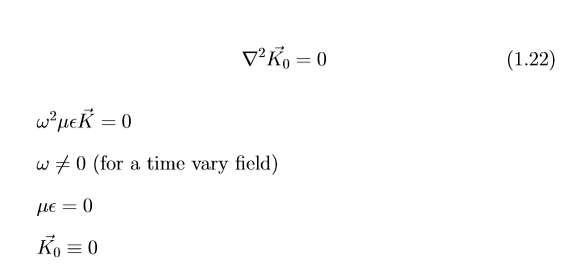
<br>
E = K = 0 Meaning no electric field at all, in other words a uniform electric field is not consistent with the maxwell’s equation. So if we are talking about time varying field, then uniform electric field in three dimensional space is not consistent with the wave equation or maxwell’s equation.
Therefore a uniform three dimensional time varying fields can not exist.
<br>
### Case 2:
Let say the electric field (E) is in all three dimensional space but uniform in a plane and let us choose a co-ordinate plane in such a way that the field is oriented in the x-axis, without loosing sense of generality, we have define which way the co-ordinate system is and which direction the electric and magnetic field are oriented. So we have the freedom to choose the co-ordinate system such that x-axis is oriented in the direction of the electric field.
<br>
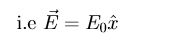
<br>
In this case we are assuming that the electric field E is constant in the direction of x-plane or a plane perpendicular to x-plane, let us consider the former. For variation of E in the yz plane and the other in the xz plane. E is uniform in xy plane or z plane. Now for variation in yz or xz plane, let us use the xz plane only and say E is dependent only on x for variation instead of (x and z) to simplify the problem. So we have E = E(x)x, if this is the solution.
<br>

<br>
Note: E = E(x)x is uniform in the yz plane only but not uniform in the xy and xz plane. With jωµH = 0, in time varying field ω not = 0, ω not = 0, =⇒ H = 0. That means this electric fields would exist without any magnetic field. However we know from maxwell’s equation that electric and magnetic field are coupled, so if the magnetic does not exist in time varying case, then the electric field can not also exist. Since there are no magnetic field in this case, electric field can not exist, so the electric field E is identically zero.
So the electric fields is uniform in a plane perpendicular to its orientation, then the field has to be identically zero because the magnetic field is identically zero. So we use the second conclusion that the electric field which is uniform in a plane perpendicular to the x-direction can not exist in an unbound medium. Let us consider the third possibility.
<br>
### Case 3:
E is uniform in a plane containing the E vector. Let us assume this is constant in the x-y plane and have variation only in the z-direction E = E0(z)x unlike the previous case, E is a function of z so ∂/∂z not = 0 , but ∂/∂x and ∂/∂y = 0, so the ∇×E = −jωµH
<br>
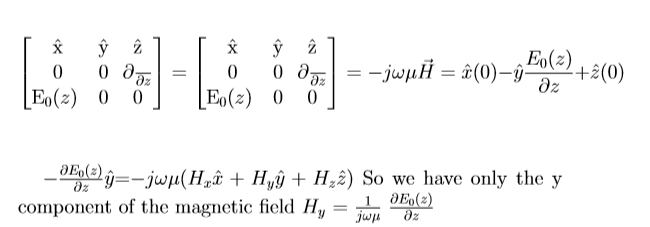
<br>
So if we consider electric field oriented in the x-direction and assume that it is constant in the x-y plane, then the corresponding magnetic field is oriented in the y-direction yet the magnetic field do exist but in the previous two cases, the magnetic field did not exist. We saw that the electric field did not satisfy the wave equation for time varying field, E was identically zero. In the second case when the electric field was constant in a plane perpendicular to its direction, it did not have a corresponding magnetic fields, because magnetic field was partially zero. For that same reason electric field for time varying field had to be zero. In this particular case however, we find that for the electric field which is oriented in the x direction and varies in the z direction i.e constant in the x-y plane, has a corresponding magnetic field and since E is a function of z i.e E is not constant as a function of z, the quantity ∂Ez/∂z is a finite quantity .
We have a magnetic field Hy = 1 jωµ ∂E0(z)/∂z associated with an x oriented electric field, so we now have three important conclusions. First, that time varying fields with uniform fields in three dimensions space can not exist. Secondly, a field which is constant in a plane perpendicular to its direction also can not exist if the fields are time varying. So the simplest possible fields which can exist in this medium are the ones which are constant in a plane in the direction of the vector fields. So in general we state that if the field which is constant in any plane, perpendicular to that plane, the field has variation and electric and magnetic field will coexist in that medium. That is why for time varying field, this is the simplest solution. We can now proceed to get the solution of the wave equation on this particular case. So we have an electric field oriented in the x direction and it’s a function of z only. E = E(z)x with e^(jωt) being implicit, hence not explicitly added to the expression as we said earlier. We substitute the field in the wave equation to be ∇^(2)E = −ω2µε E since we have only the x component in E, the equation should be satisfied by the x component.
<br>
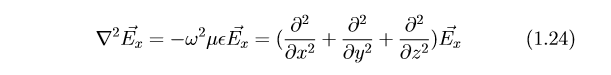
<br>
Hence E is a function of z only. ∂^(2)/ ∂x^(2) and ∂^(2)/∂x^(2) = 0 and ∂^(2)Ex/∂z^(2) =−ω2µεEx but since E is not varying as a function of x and y, so Ex is a function of z only, so that we replace the partial derivative with the full derivative we got.
d^(2)Ex/ dz^(2) =−ω2µεEx this is identical to the transmission line equations we have solved for and it is now 1-dimensional case. So we are simply saying that Ex is now a scaler quantity. So if we replace Ex by V, we get the equation for transmission line. So this case the simplest solution which we get in unbound medium is identical to the solution which we get for the transmission line. Since we have investigated transmission line in details, most of the concept which we have done for transmission line will be applied to this case also. So in transmission line when we are investigating, we define the quantity −ω2µε as (propagationconstant)^2, so with the same understanding, we can call −ω2µε as propagation constant squared. So following the convention and notation which we have for transmission line, we define γ^2=−ω^(2)µε or γ=p−ω2µepsilon = jω√µ. If we go by the way γ was defined ealier, γ=α + jβ, then α was attenuation constant and β = phase constant. So that γ=α + jβ = jω√µε, this means that for this case α which is attenuation constant is zero and β=jω√µε. We recall in transmission line that α = 0, this represents a lossless transmission line, what this physically means was that when the wave travels on the transmission line, the amplitude of wave does not decrease, it has a constant amplitude, this is same thing that represented here. In this case the solution of the wave equation is identical to the transmission line solution with Ex for V and the amplitude of the wave should not vary as a function of the distance i.e in the direction z. So this represent now in terms of transmission line terminology that we developed, a lossless propagation on the transmission line and the solution which we have gotten from the transmission line is a second order differential equation after defining the parameter is
<br>
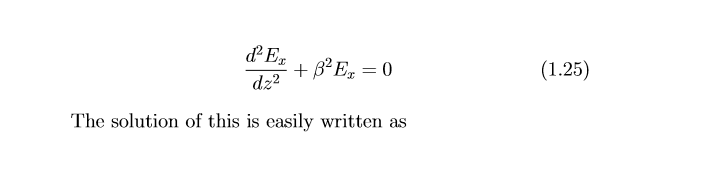
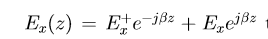
<br>
This similar to transmission line for simplest case of wave propagation in an unbound medium. We get electric field which is a combination of E^(+)x and E^(-)x and we know from transmission line earlier that E^(+) x e−jβ represents a forward travelling wave in the z-direction and E^(−) x e^(−jβ) represents a backward travelling wave in the in the -z direction. So we get solution for the electric field which is a combination of two travelling waves of amplitude E^(+) x and E^(−) x travelling in opposite direction in positive z-direction and negative z-direction.
_____
## <center> ALL IMAGES ARE 100% ORIGINAL AND WAS DESIGN WITH LATEX TO ENABLE ME GET THE RIGHT SYMBOL FOR THE EQUATIONS </center>
_______
#### Reference
* <i><sub>https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&cad=rja&uact=8&ved=0ahUKEwjP64u8zMvZAhWGL8AKHeYzBkYQFggzMAI&url=http%3A%2F%2Fwww.ece.rutgers.edu%2F~orfanidi%2Fewa%2Fch01.pdf&usg=AOvVaw0fOP37LkeBtsK5SERkOajq</sub><i>
* http://www.nptel.ac.in/courses/117101057/ScientificWord/CHAP%204.html
* https://www.electronicshub.org/electromagnetic-waves/
_____

<i>[my little design]</i>
 hiveblocks
hiveblocks