Hello friends of steemit, continuing with my publication referring to the science of mathematics and the whole that make it up, today I want to make reference in this post about the quadratic function and all the elements that comprise it, properties, graphic elements, equations in general and also supplement this information with examples of this function.
# <center>Quadratic Function</center> #
In mathematics, a quadratic function of a variable is a polynomial function defined by:
<center>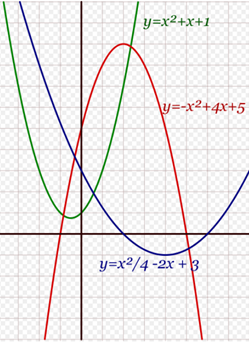</center>
### <center>quadratic function graph</center> ###
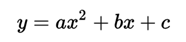
With 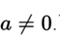 It is also the case that it is called quadratic trinomial. Also functions called quadratic functions defined by quadratic polynomials of more than one variable, for example:
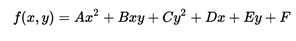
In this case, the set of points that result from equating the polynomial to zero represent geometric places that it is always possible to reduce to one of the forms:
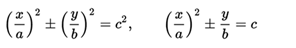
### That correspond to three types of conic sections (ellipse, hyperbola and parabola). ###
# Quadratic functions of a variable #
The graphs of these functions correspond to vertical parabolas (axis of symmetry parallel to the axis of the ordinates), with the peculiarity that when a> 0, the vertex of the parabola is in the lower part of it, being a minimum ( that is, the parabola opens "upwards"), and when a <0 the vertex is at the top, being a maximum (that is, the parabola opens "down").
The study of the quadratic functions has numerous applications in very diverse fields, for example the free fall or the parabolic shot.
The function derived from a quadratic function is a linear function and its indefinite integral is a family of cubic functions.
## Estate ##
The roots (or zeros) of a quadratic function, as in every function, are the values of x, for which 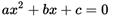they are usually denoted as: X1 and X2,depending on the value of the discriminant Δ defined as 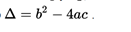.
- Two real and different solutions if the discriminant is positive, 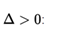
<center>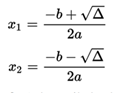</center>
- Cut the parabola to the X axis at two different points.
- A real solution (or double solution) if the discriminant is zero, 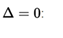
<center>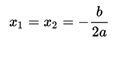</center>
- The parabola is tangent to the X axis.
- The parabola does not cut the X axis.
- The only remaining case is that the discriminant is negative, < 0
In this case, the roots are not real, but they are two complex conjugated numbers:
<center>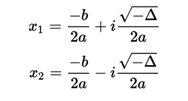</center>
# Analytical Representation #
There are three ways to write a quadratic function, applicable according to the use that you want to give the function, an analytical study of the function or the quadratic equation, an interpretation or geometric construction of the parabola, etc.
### Developed or polynomial form ###
The developed form of a quadratic function (or standard form) corresponds to that of the second-degree polynomial, written as:
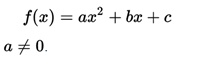
### Factored form ###
All quadratic functions can be written in factored form according to their roots as:
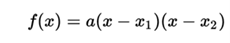
being to the main coefficient of the function X1 and X2 the roots of f (x). In the case that the delta discriminant is equal to 0 then X1 = X2, so the factorization acquires the form:
<center>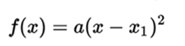</center>
In this case a is called double root, since its multiplicity order is. If the discriminant is negative, the solutions are complex, factoring is not possible.
### Canonical form ###
Every quadratic function can be expressed by the square of a binomial in the following way:
<center>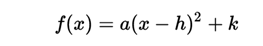</center>
being the main coefficient and the ordered pair (h, k) the coordinates of the vertex of the parabola.
### Translation ###
From the primitive function, we can obtain different displacements (translation) of the functions, these can be given in two directions: Horizontal (on the axis of the x) or Vertical (on the axis of the y).
The function y = x2 is the primitive function of the quadratic function, from which we can then obtain the functions whose graphs are displaced on the x and y .
For horizontal displacements we work with functions of the form 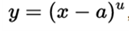, which follow the rule of:
- A greater a corresponds to a horizontal shift to the right.
- A minor a corresponds to a horizontal shift to the left.
- For vertical displacements we work with functions of the form 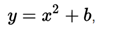who follow the rule of:
- A greater b corresponds a vertical displacement upwards.
- A smaller b corresponds to a vertical downward displacement.
# Graphic representation #
<center>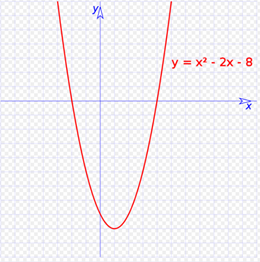</center>
#### <center>Intersection with the y</center> ####
The function cuts the y-axis at the point y = f (0), that is, the parabola cuts the y-axis when x is zero (0):
<center>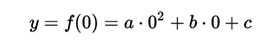</center>
what results :
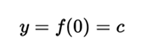
the function cuts the y at the point (0, c), where c is the independent term of the function.
At this point of the function it is also known with Order of Origin, since it is given in the terms.
#### Intersection with the x ####
The function cuts to the x axis when y is 0, given the function
<center>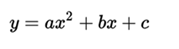</center>
that is to say :
<center>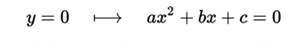</center>
the different solutions of this second degree equation are the cases of cutting with the x axis, which are obtained, as is known, by the expression:
<center>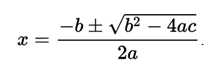</center>
#### If the function does not cut the x-axis, the previous formula has no real solution. It may happen that it does not have intersections with the x . ####
## Extreme ##
In principle, in math, the maximum and the minimum are designated as extreme, for example in the set S = {1,5,9, 13, 17} the minimum is 1 and the maximum is 17, and the extremes are 1 and 17 To calculate the end of a quadratic trinomial, we can use a theorem, approachable in elementary algebra, based on the behavior of a sum of a square of a variable with any real number.
### Fundamental theorem of the quadratic trinomial ###
The real quadratic trinomial
<center>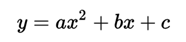</center>
it has an extreme value that it achieves when
<center>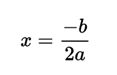</center>
#### this value is minimal if a> 0, maximum if a <0. If ymax exists, ymin does not exist, and vice versa.6 It will be abbreviated as TFTC. ####
### Problem 1 ###
Decompose the positive number s, in two addends, in such a way that the product of them is maximum. Be one of the adding x, the other adding will be s-x and its product p = x (s-x)
## <center>p = -x2 + sx.</center> ##
Then applying the TFTC results x = s / 2; in such a case s-x = s / 2. Consequently, the product reaches the maximum value if both addends are equal. If the sum is 30 the product is reached when the summed ones are 15 and 15, whose product is 225.
### Problem 2 ###
There is a wire fence of 120 meters to fence a rectangular terrain, find the maximum area of land to be fenced. If the sides measure x, y we have 2x + 2y = 100 where y = 50-x and the area is
A = x (50-x) = -x2 + 5ox and applying the TFTC and the previous result, since the sum x + (50-x) = 50 the product A is maximum when x = 50-x, or x = 25
Then the maximum area is {\ displaystyle 25 \ times 25 = 625} {\ displaystyle 25 \ times 25 = 625}
# Differential calculation alternative #
Every quadratic function has a maximum or a minimum, which is the vertex of the parabola. If the parabola has concavity upwards, the vertex corresponds to a minimum of the function; whereas if the parabola has concavity downwards, the vertex will be a maximum.
Given the function in its developed form: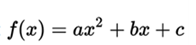 the x coordinate of the vertex will be simply: 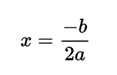The y coordinate of the vertex corresponds to the function f evaluated at that point.
Given the canonical form: 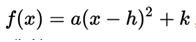 the explicit coordinates of the vertex are: (h, k)
the derivative of the function, and is equal to zero, the solution to this equation are the possible maximums and minimums of the function, in this case, starting from the quadratic function:
<center>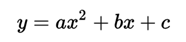</center>
we calculate its derivative with respect to x:
<center>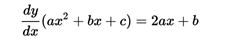</center>
that if we equate it to 0, we have:
<center>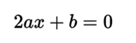</center>
where x will be worth:
To know if it is a maximum or a minimum it is necessary to see the second derivative of the function, let's see:
<center>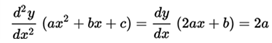</center>
this is: 2a will be positive when a is positive and negative if a is negative, therefore, if the second derivative 2a is positive the parabola is concave and the point will be a minimum of the function, if a is negative the parabola will be convex and be a maximum.
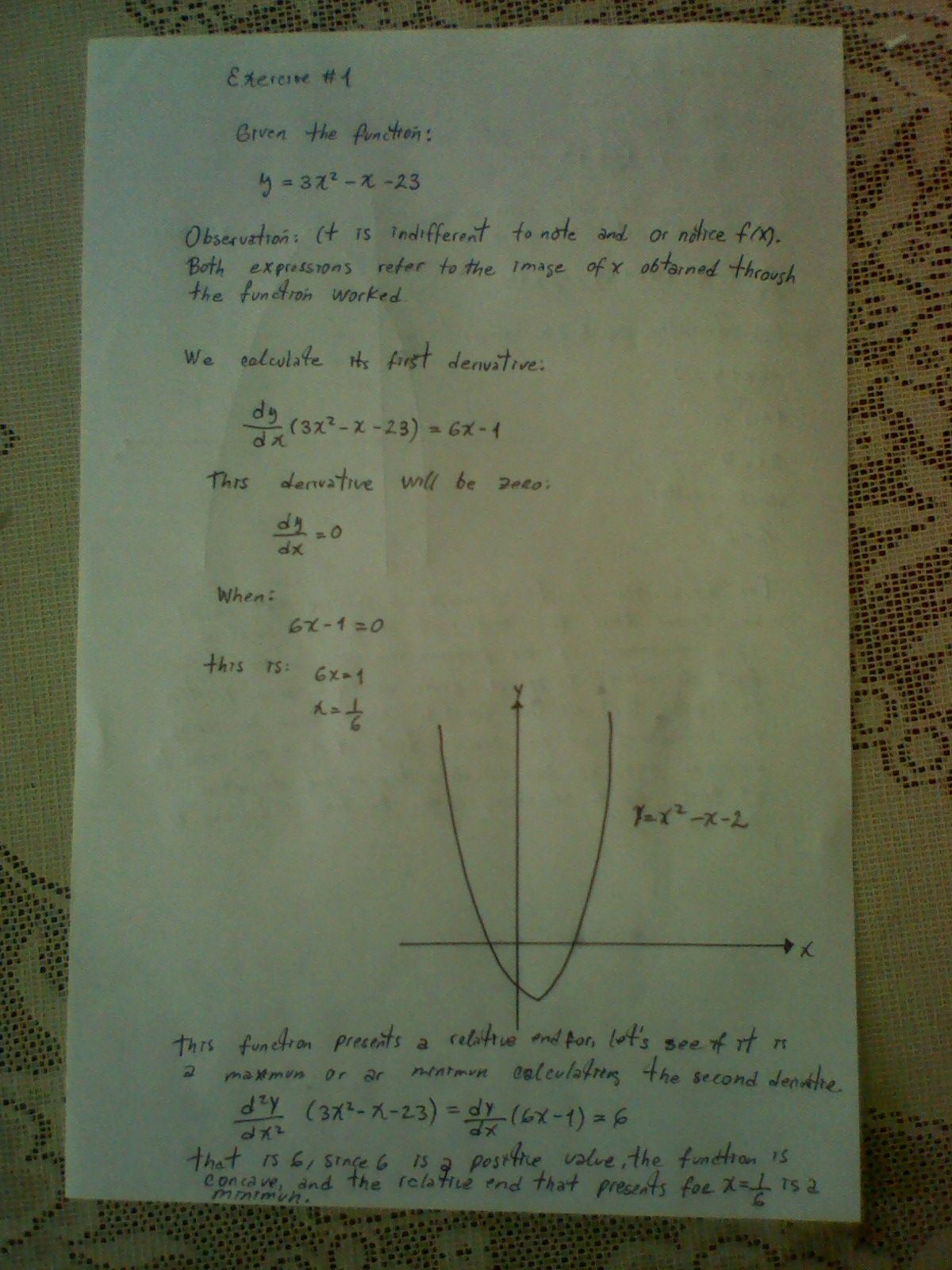
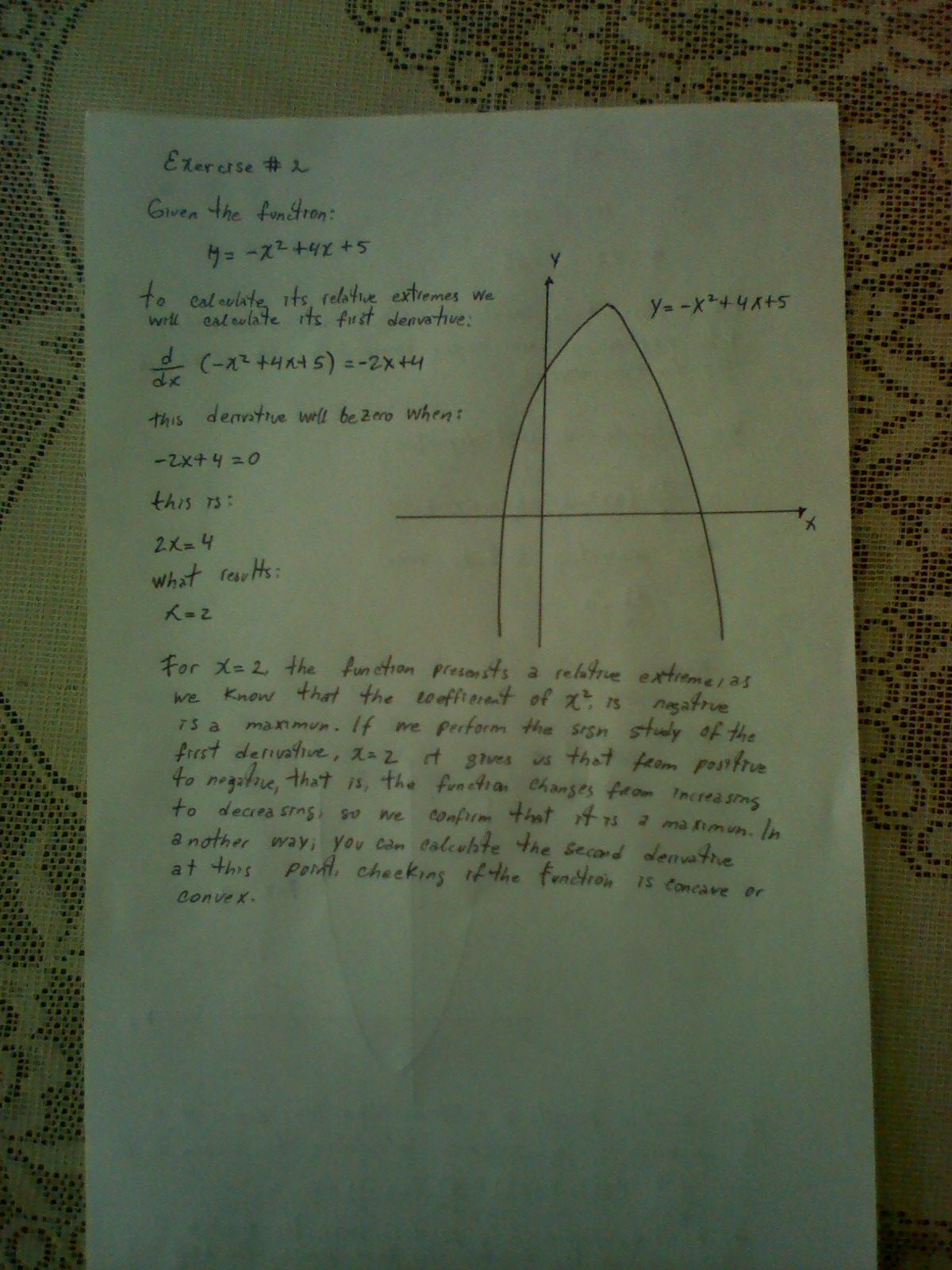
## Example of exercises, applying the quadratic function, with its fundamental elements and its respective graph. ##
### Bibliography : ###
Epsilon Group, ed. (9 of 1994). Study of functions: the quadratic function (1 edition). Bancaja Foundation. Gallego Palomero (7 of 1989). Quadratic function (1 edition). SM editions.
### References : ###
Lehmann: Algebra, Limusa Wiley, Máxico D-F.
I.P. Natansón Elementary problems of maximum and minimum Sum of infinitely small quantities, Editorial Mir, Moscow (1977)
There is no sense in the presence of complexes, it is a real variable real function
Algebra and elementary functions. Alexandrov and others, editorial Mir.
Haaser- Lasalle- Sulivan. Mathematical Analysis I hiveblocks
hiveblocks