<center></center>
Hello all steemians. It's me @leoumesh and today I am gonna be giving a very brief introduction on quadratic equation.
So lets start.
<h1>1. What is Quadratic Equation?</h1>
In the above word we can see one word i.e. **"quad"** whose meaning means square. And the variable gets squared in the quadratic equation. So, a quadratic equation is basically a polynomial equation whose general form is:
<center><h2>**ax<sup>2</sup>+bx+c=0**</h2></center>
where,
i. a,b and c are known values and a≠0 i.e. the value of a cannot be zero
ii. x is a variable and its value is unknown.
Quadratic equation for this reason is also known as ***"Equation of Degree 2"***. The examples of quadratic equation are:
1. x<sup>2</sup> + 5x + 6 = 0
Here a=1, b=5 and c=6
2. 2x<sup>2</sup> - 3x - 2 = 0
Here a=2, b=-3 and c=-2
<h1>2. Graph For Quadratic Equation</h1>
<center>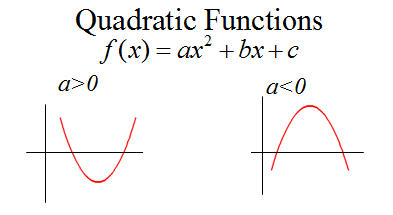</center>
<center><a href="https://wwwi.scottsdalecc.edu/softchalk/math/quadratics/Quadratics_print.html">Source : scottsdalecc</a></center>
The graph for any quadratic equation is parabolic in nature which can be of two forms : concave up(left side of figure) or concave down(right side of figure). Its parabolic concave up or down nature is determined by the value of a in the equation ax<sup>2</sup>+bx+c=0. If a>0 then the graph for quadratic equation is parabolic concave up otherwise parabolic concave down.
<h1>3. Roots of Quadratic Equation</h1>
So, what basically means a root? Any real number value that satisifes a given quadratic equation or gives a solution is called roots. By real number we are referring to real number value of x. In the above figure, we can see that the two ends of parabola have cut X-axis at two points. Quadratic equation gives exactly two roots. So the roots of quadratic equation are exactly these x-intercepts (the intersection of graph of quadratic function and x-axis).
The following derivational process gives a roots of quadratic equation whose form is **ax<sup>2</sup>+bx+c=0**. So basically for finding these roots we use a method known as ***"Solving By Completing The Square"***.
<br>
First, we divide the both sides of the equation by a so as to make the coefficient of x<sup>2</sup> as 1,
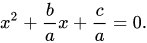
Now, we send c/a to right hand side of the equation,
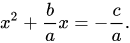
To reduce left handside to (a+b)<sup>2</sup>, we add (b/2a)<sup>2</sup> to both sides of equation,
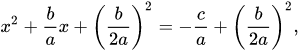
The left side is written in square form and evaluate 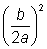 as 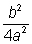
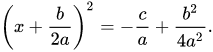
The LCM of a and 4a<sup>2</sup> is 4a<sup>2</sup>. So, c is multiplied by 4a since in denominator there is a and we need to multiply it by 4a to make it 4a<sup>2</sup>. After then we rearrange it.
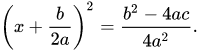
We then use square root property. Remember we always want positive and negative square roots.
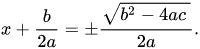
 is sent to right side so as to isolate x,
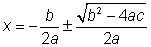
Now we add the fraction since they have common denominator and obtain formula for root as,
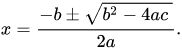
Don't get confuse with **plus-minus symbol "±"** symbol. It implies that:
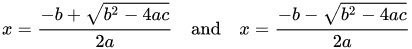
The use of the plus and the minus signs give the two roots of the quadratic equation.
<br>
<h1>4. The quadratic equation ax<sup>2</sup>+bx+c=0 cannot have more than two roots.</h1>
If possible, let, α, β and γ be three different roots of the quadratic equation:
<center><h2>**ax<sup>2</sup>+bx+c=0**</h2></center>
Then since each of these values must satisfy the equation, we have,
<center><h2>aα<sup>2</sup> + bα + c = 0 ............... (i)</h2></center>
<center><h2>aβ<sup>2</sup> + bβ + c = 0 ............... (ii)</h2></center>
<center><h2>aγ<sup>2</sup> + bγ + c = 0 ............... (iii)</h2></center>
Subtracting (ii) from (i), we get,
<center><h2>a(α<sup>2</sup>-β<sup>2</sup>)+b(α-β)=0</h2></center>
Since α≠β, divide out by α-β, then,
<center><h2> a(α + β) + b = 0............... (iv) </h2></center>
Similarly, subtracting (iii) from (ii), we get,
<center><h2>a(β + γ) + b = 0............... (v) </h2></center>
Now, subtracting (v) from (iv),we get,
<center><h2>a(α - γ) = 0</h2></center>
which is impossible, since by hypothesis a≠0 and α is not equal to γ. Hence there cannot be more than two roots.
<br>
<h1>5. Nature of Roots of Quadratic Equation</h1>
Let the roots of the quadratic equation:
<center><h2>**ax<sup>2</sup>+bx+c=0**</h2></center>
where a≠0, be denoted by α and β, so that
α=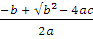 and β=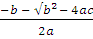
(***Note that the constants a,b,c are rational numbers here.***)
The expression b<sup>2</sup>-4ac, under the radical sign, occurs in both the roots. Its value depends on the coefficients a,b and c. There are three possibilities:
I. If **b<sup>2</sup>-4ac>0**, (the quantity under the radical sign is positive), then the roots are real and unequal.
In particular, if **b<sup>2</sup>-4ac** is positive as well as a perfect square, the roots are rational and unqequal, provided a,b and c are rational.
II. If **b<sup>2</sup>-4ac=0**, then the roots are real and equal each being -b/2a.
III. If **b<sup>2</sup>-4ac<0**, then the roots are imaginary and unequal.
Thus computing the value **b<sup>2</sup>-4ac**, it is possible to determine the nature of the quadratic equation without actually solving the equation. This quantity is therefore known as the ***discriminant of the quadratic equation***.
In the following example:
<center><h2>**2x<sup>2</sup>-3x-2=0**</h2></center>
Comparing it with standard equation **ax<sup>2</sup>+bx+c=0**, we get,
a=2
b=-3,
c=-2, and
b<sup>2</sup>-4ac=25>0, therefore the roots are real, rational and unequal.
<br>
<h1>6. Relation Between Roots and Coefficients of Quadratic Equation</h1>
Let the roots of the quadratic equation:
<center><h2>**ax<sup>2</sup>+bx+c=0**</h2></center>
where a≠0, be denoted by α and β, so that
α=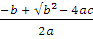 and β=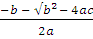
We have, by addition
α + β = 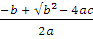 + 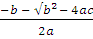
or, α + β = 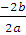 = - b/a
i.e. α + β = - 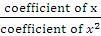
<br>
Again, by multiplication, we have
α * β = 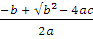 * 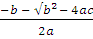
or, α * β =
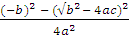
or, α * β = 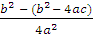
or, α * β = 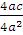 = 
i.e α * β = 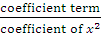
**Therefore, the sum of the roots = -b/a**
**Therefore, the product of the roots = **
***Note : - In a quadratic equation where the coefficient of x<sup>2</sup> is unity,***
I. the sum of the roots is equal to the coefficient of x with its sign changed.
II. the product of the roots is equal to the coefficient term or constant term i.e. c.
<br>
<h1>7. Special Roots of Quadratic Equation</h1>
Under the following conditions the given quadratic equation will have the special roots:
I. **Roots equal in magnitude but opposite in sign:**
Two roots will be equal in magnitude but opposite in sign if their sum is zero
<center>**α + β = -b/a = 0**</center>
<center>**i.e. b = 0**</center>
II. **Reciprocal roots :**
The two roots will be reciprocal to each other if their product is 1.
<center>**α * β =**  = 1</center>
<center>**i.e. c = a**</center>
III. **One root zero :**
If one root is zero, then the product of the root is zero.
<center>**i.e.  = 0**</center>
<center>i.e. c = 0</center>
III. **Both root zero :**
If both roots are zero, then
<center>**α + β = -b/a = 0**</center>
<center>**i.e. b = 0**</center>
<center>**Also  = 0**</center>
<center>i.e. c = 0</center>
Therefore, b = 0 and c = 0
<br>
<h1>8. Formation of Quadratic Equation</h1>
Suppose ***ax<sup>2</sup> + bx + c =0*** is the required equation, and α and β are the given roots.
The equation may be written as
<center>**x<sup>2</sup> + ( b / a ) x + ( c / a ) = 0** </center>
<center>or, **x<sup>2</sup> - ( α + β ) x + α * β = 0**</center>
(This is because α + β = -b /a , α * β =  )
Hence any quadratic equation may be expressed in the form
<center>**x<sup>2</sup> - ( sum of the roots ) x + product of the roots = 0**</center>
**Example : Lets find the equation whose roots are 2 and -3**
Here, we have the sum of roots = 2 + (-3) = 2 - 3 = -1
products of the roots = 2 * (-3) = -6
The equation is given by x<sup>2</sup> - ( sum of the roots ) x + product of the roots = 0
**So the equation is x<sup>2</sup> + x - 6 = 0**
<br>
<hr>
**Another Example**
Lets find the root of the quadratic equation:
<center> **x <sup>2</sup> + x - 20 = 0**</center>
Comparing this equation with standard quadratic equation ***ax<sup>2</sup> + bx + c =0***, we get,
<center>**a = 1**</center>
<center>**b = 1 , and**</center>
<center>**c = -20**</center>
So the roots are given by :
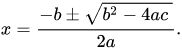
Taking " + " ,
<br>
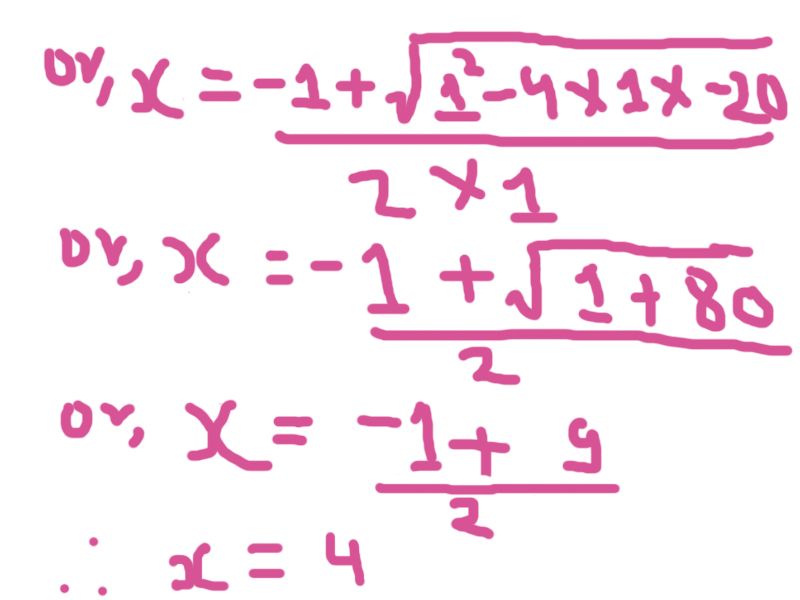
<center>***Done from Adobe Photoshop CS6***</center>
<br>
Similarly taking " - ",
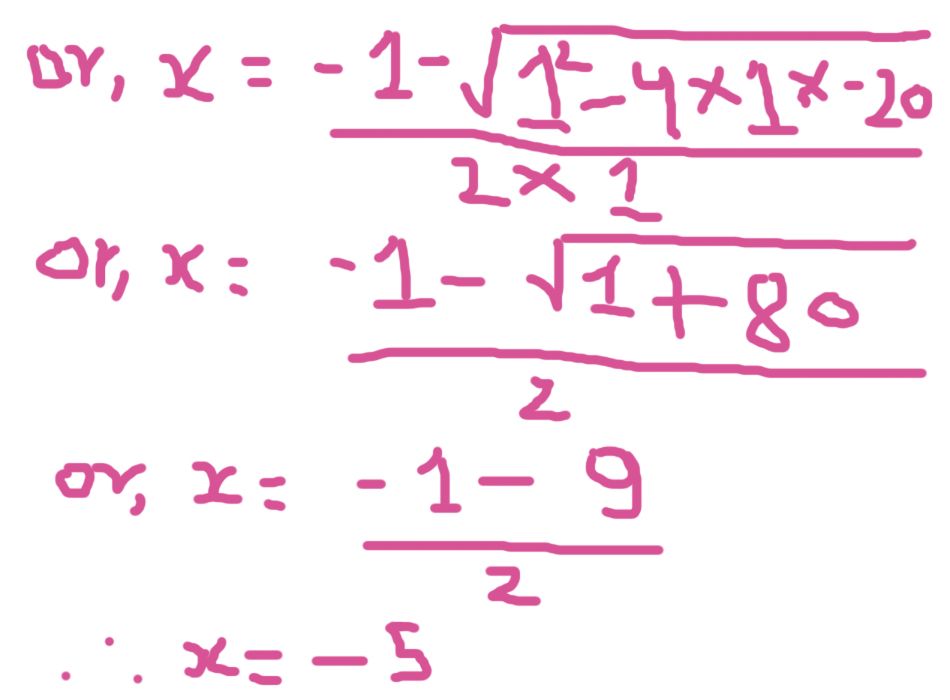
<center>***Done from Adobe Photoshop CS6***</center>
Hence the two roots of quadratic equation are 4 and - 5.
Lets find the nature of roots, sum of the roots and product of the roots.
I. **Nature of roots**
Here b<sup>2</sup> - 4ac = 1<sup>2</sup>- 4 * 1 * ( - 20 ) = 1 + 80 = 81
**i.e. b<sup>2</sup> - 4ac > 0, so the roots are real and unequal.**
<br>
II. **Sum and Product of Roots**
Sum of roots= - b / a = -1 / 1 = - 1
Product of roots =  = - 20 / 1 = -20
III. **Graph of the equation**
<center>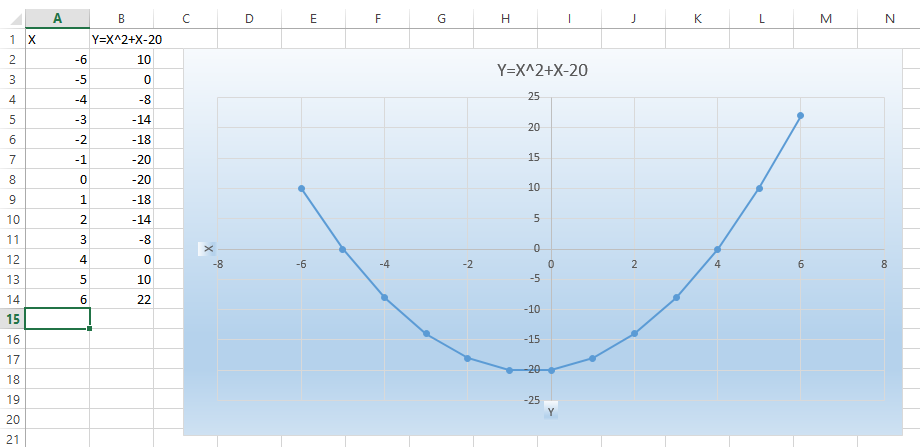</center>
<center>**Plotted in MS Excel**</center>
As stated earlier, the nature of quadratic equation graph is parabolic.
Here a= 1 > 0 , so the parabolic curve is concave up.
The parabolic curve intersects the x-axis at two points -5 and 4. These are the roots of quadratic equation or the values that satisifies the given quadratic equation.
<br>
***So, this is all basic about quadratic equation. Please feel free to leave a comment. Thank you.***
<h1>References</h1>
1. https://en.wikipedia.org/wiki/Quadratic_formula
2. https://wwwi.scottsdalecc.edu/softchalk/math/quadratics/Quadratics_print.html
3. https://www.mathsisfun.com/algebra/quadratic-equation.html
<h3>steemstem:</h3>
<center></center>
SteemSTEM is a community driven project which seeks to promote well-written and informative Science, Technology, Engineering and Mathematics posts on Steemit. The project involves curating STEM-related posts through upvoting, resteeming, offering constructive feedback, supporting scientific contests, and other related activities.
DISCORD: https://discord.gg/j29kgjS
 hiveblocks
hiveblocks