Hello and a warm and lovely greetings to all steemians. It's me @leoumesh and today I am gonna be continuing with the rest of topics related to sequence and series. If you are unfamiliar with this one, please [Click Here](https://steemit.com/steemstem/@leoumesh/sequence-and-series-a-simple-introduction) to visit previous article where I had made an introductory explanation on sequence and series, their types along with formulae.
So lets begin with the rest of our topic.
<center></center>
<center>***Designed from Adobe Photoshop CS6***</center>
<br>
<h1>I. Arithmetico-Geometric Series</h1>
The terms of an AS are:
<center>*a , a+d , a+2d , a+3d , .......*</center>
The terms of a GS are:
<center>1 , *r , r<sup>2</sup> , r<sup>3</sup> , .....* </center>
A series of the type
<center>*a*.1 + *(a+d)r + (a+2d)r<sup>2</sup> + (a+3d)r<sup>3</sup> + .....* </center>
whose each term is the product of the corresponding terms of an AS and a GS is known as the ***arithmetico-geometric*** series
The following example will illustrate what is arithmetico-geometric series:
<center>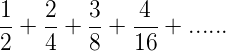</center>
The given series may be written as follows:
<center>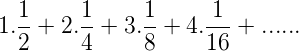</center>
Clearly, the above series is the arithmetic-geometric series with common difference = 1 and common ratio = 
<h2>General Term of Arithmetico-Geometric Series</h2>
In the sequence
<center>*a*.1 + *(a+d)r + (a+2d)r<sup>2</sup> + (a+3d)r<sup>3</sup> + .....* </center>
The *n<sup>th</sup>* term of arithemtico-geometric series is given by multiplying the corresponding general terms of the arithmetic sequence (AS) and the geometric sequence (GS) as,
<center>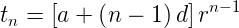</center>
<h2>Sum of n terms</h2>
The sum of *n* terms of arithmetico-geometric series is given by,
<center>S<sub>n</sub> = 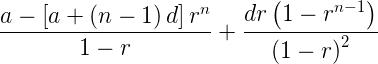</center>
<br>
<h1>II. Sum of the Natural Numbers</h1>
The numbers 1 , 2 , 3 , 4 , ..... are said to be the natural numbers. Now , we derive some of the formulae for the sum of the first *n* natural numbers, the sum of the squares of the first *n* natural numbers and the sum of the cubes of the first *n* natural numbers.
<br>
<h2>1. Sum of the first ***n*** natural numbers</h2>
The first ***n*** natural numbers are 1 , 2 , 3 , ....... , n
<center>Let , 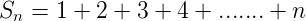</center>
The sum of first n terms of the arithmetic series is given by S<sub>n</sub> = 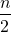[2a+ (n -1 )d]. So,
<center>S<sub>n</sub>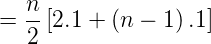</center>
<center>or, S<sub>n</sub> = 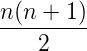</center>
<center>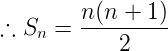</center>
<br>
<h2>2. Sum of the first ***n*** even natural numbers</h2>
The first ***n*** even natural numbers are 2 , 4 , 6 , ...... , n terms
<center>Let , 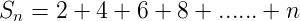</center>
<center>or, 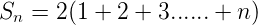</center>
<center>or, 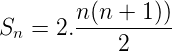</center>
<center>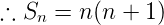</center>
<br>
<h2>3. Sum of the first***n*** odd natural numbers</h2>
The first ***n*** odd natural numbers are 1 , 3 , 5 , ...... , n terms
<center>Let , 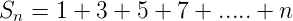</center>
The sum of first n terms of the arithmetic series is given by S<sub>n</sub> = 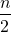[2a+ (n -1 )d]. So,
<center>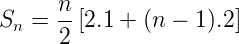</center>
<center>or, 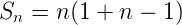 </center>
<center>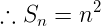</center>
<br>
<h2>4. Sum of the squares of the first ***n*** natural numbers</h2>
The sum of the squares of the first ***n*** natural numbers is given by the formula,
<center>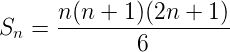</center>
<br>
<h2>5. Sum of the cubes of the first ***n*** natural numbers</h2>
The sum of the cubes of the first ***n*** natural numbers is given by the formula,
<center>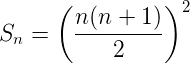</center>
The sum of the cubes of the first ***n*** natural numbers is the square of the sum of the first ***n*** natural numbers.
<br>
<h1>III. Means</h1>
A finite sequence consisting of more than two terms has one or more terms in between the first and the last terms. These terms are called the ***arithmetic , geometric or harmonic means*** according as the sequences are arithmetic , geometric or harmonic. In other words, we have the following definitions :
I. Any term in between the first and last terms of an arithmetic sequence is called an ***arithmetic mean***(AM).
II. Any term in between the first and last terms of a geometric sequence is called a ***geometric mean***(GM).
III. Any term in between the first and last terms of a harmonic sequence is called a ***harmonic mean***(HM).
<br>
<h1>**Formula for Means**</h1>
<h2>Formula 1</h2>
Given any two numbers a and b , the AM , GM , and HM between them are given by :
<center>1. AM = A = 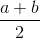</center>
<center>2. GM = G = 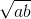</center>
<center>3. HM = H = 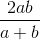</center>
<br>
<h2>Proof</h2>
1. If 'A' is the single AM between *a* and *b* , then *a* , A , *b* form an AS. Now by the defintion of an AS,
<center>A - a = b - A</center>
<center>or, 2A = a + b</center>
<center>or, A = 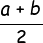</center>
<center> A = 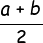</center>
2. If 'G' is the single GM between *a* and *b* , then *a* , G , *b* form a GS. Now by the definition of a GS,
<center>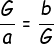</center>
<center>or, 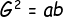</center>
<center>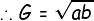</center>
3. If 'H' be a single HM between *a* and *b*, then *a* , H , *b* are in HP.
<center>i.e. 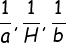 are in AP</center>
<center>Hence, 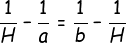</center>
<center>or, 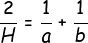</center>
<center>or, 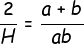</center>
<center>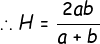</center>
<br>
<h2>Formula 2</h2>
Given any two numbers *a* and *b* , the *n* AM's between them are given by,
<center>*a + d , a + 2d , a + 3d , a + 4d , ........ , a + nd*</center>
where , <center>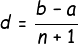</center>
<h2>Proof</h2>
Let ***m<sub>1</sub> , m<sub>2</sub> , m<sub>3</sub> , ........... , m<sub>n</sub>*** be *n* AM's to be inserted between *a* and *b*. Then,
<center>***a , m<sub>1</sub> , m<sub>2</sub> , m<sub>3</sub> , ........... , m<sub>n</sub> , b*** are in AP</center>
The number of terms in the above AS is *n*+2 of which the first term is *a* and the last term *b*, the (*n* + 2)<sup>th</sup> term of an AS.
If *d* is the common difference then
<center>*b* = *a* + (n + 2 - 1)d</center>
<center>or, *b* - *a* = (n + 1)d</center>
<center>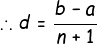</center>
Now, <center>*m*<sub>1</sub> = *t*<sub>2</sub> = *a* + *d*</center>
<center>*m*<sub>2</sub> = *t*<sub>3</sub> = *a* + 2*d*</center>
<center>*m*<sub>3</sub> = *t*<sub>4</sub> = *a* + 3*d*</center>
<center>.... ..... ..... .....</center>
<center>.... ..... ..... .....</center>
<center>*m<sub>n</sub>* = *t<sub>n+1*</sub> = *a + nd*</center>
<br>
<h2>Formula 3</h2>
Given any two numbers *a* and *b* , the *n* GM's between them are given by *ar , ar<sup>2</sup> , ar<sup>3</sup> , ..... , ar<sup>n</sup>, where 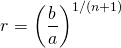
<h2>Proof</h2>
Let G<sub>1</sub> , G<sub>2</sub> , G<sub>3</sub> , ...... , G<sub>*n*</sub> be *n* GM's between *a* and *b* then,
<center>*a* , G<sub>1</sub> , G<sub>2</sub> , G<sub>3</sub> , ...... , G<sub>*n*</sub> , *b* form a GS</center>
The number of terms in the above GS is (*n*+2) of which the first term is *a* and the last term *b* , the (*n*+2)<sup>th</sup> term of a GS.
If *r* be the common ratio then ,
<center>b = ar<sup>*n*+ 2 - 1</sup></center>
<center>or, b = ar<sup>n + 1</sup></center>
<center>or, 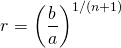 </center>
Now, <center>G<sub>1</sub> = *t<sub>2</sub>* = *ar*</center>
<center>G<sub>2</sub> = *t<sub>3</sub>* = *ar*<sup>2</sup></center>
<center>G<sub>3</sub> = *t<sub>4</sub>* = *ar*<sup>3</sup></center>
<center>.... ..... ..... .....</center>
<center>.... ..... ..... .....</center>
<center>G<sub>*n*</sub> = *t<sub>n + 1</sub>* = *ar*<sup>n</sup></center>
<br>
<h2>Formual 4</h2>
The AM , GM , HM between any two unequal positive numbers satisfy the following relations :
1. ( GM )<sup>2</sup> = ( AM ) * ( HM )
2. AM > GM > HM
<h2>Proof</h2>
Let *a* and *b* be two unequal positive numbers. Then,
<center>AM = 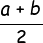</center>
<center>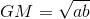 ( only positive square root is taken )</center>
and, <center>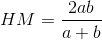</center>
To prove the first part, we have
<center>AM * HM = 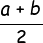 * 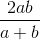</center>
<center>or, 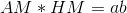</center>
<center>or, 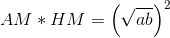</center>
<center> AM * HM = ( GM )<sup>2</sup></center>
This result shows that GM is again the geometric mean between AM and HM.
To prove the second part , consider
AM - GM = 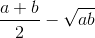
or, AM - GM = 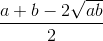
or, AM - GM = 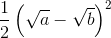
Which is always positive as we have squared the term.
<center>Hence, AM > GM</center>
Again,<center> ( AM ) * ( HM ) = ( GM ) * ( GM )</center>
<center>or, 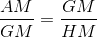</center>
<center>Since , AM > GM</center>
</center>We have, GM > HM</center>
Combining the two , we have
<center>AM > GM > HM</center>
This result shows that AM , GM and HM are in decreasing order of magnitudes.
<hr>
<br>
***Thank you for taking your time in reading this article. Please feel free to comment and interact.***
<hr>
<br>
<h1>References</h1>
1. https://www.aplustopper.com/arithmetico-geometric-sequence/
2. https://www.careerbless.com/aptitude/qa/sequence_series_imp.php
3. Mathematical expression coded on : http://www.quicklatex.com/
<hr>
<br>
<h1>steemstem</h1>
<center>https://steemitimages.com/DQmW9GJdsBreapMb5csEow9rj9LCv1CbcZ52rrfttHyzQXs/ylp.gif</center>
**SteemSTEM is a community driven project which seeks to promote well-written and informative Science, Technology, Engineering and Mathematics ( STEM ) posts on Steemit. The project involves curating STEM-related posts through upvoting, resteeming, offering constructive feedback, supporting scientific contests, and other related activities.**
DISCORD: https://discord.gg/j29kgjS
 hiveblocks
hiveblocks