In the next few posts, we will have an in-depth look at <strong>power functions</strong>. These are functions where the dependent variable <em>x</em> is raised to the power <em>a</em>. That is, they are of the form...

<center>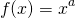![c20.png](https://steemitimages.com/DQmdAigvVtorSzkRBcy9mEaLXEMUgYyk6XwRNYuhcvKTjQa/c20.png)</center>

<strong>Case 1.</strong> The power <em>a</em> = <em>n</em>, where <em>n</em> is a positive integer. That is...

<center>![c1.png](https://steemitimages.com/DQmXa1TTMDb1K9j6jbp2gfqt2CHRH72MPgcbDfgpfkvrAU1/c1.png)</center>

These are <a href="https://steemit.com/steemiteducation/@masterwu/what-are-polynomial-functions">polynomial functions</a> of degree <em>n</em> with only one term. Graphs with increasing powers are shown in the tables below...

<table>
<tr>
<td><center>https://steemitimages.com/DQma9QnCg1ZfHPz7cvHb1Sz1Ly8NSmJYxWKqTC2NGkdbAHm/c3.png</center></td>
<td><center>https://steemitimages.com/DQmeoK61fZd6kE7xhA9TbhGbCrUfyF5zVWax8T4dKZB2zNa/c5.png</center></td>
</tr>
<tr>
<td><center>https://steemitimages.com/DQmaVyp3gS7essP7BgTXQyJnsBsedqmL7cpxuxbefw2sxii/c7.png</center></td>
<td><center>https://steemitimages.com/DQmWnAPYazTptRdpj2AtLyM3aMnd4YgnEAfbomSTiFze3Z6/c9.png</center></td>
</tr>
<tr>
<td><center>https://steemitimages.com/DQmdL5GgZzbTydmiji1YJwzUzXuVdmW7ya2D46hgw8sUZAB/c11.png</center></td>
<td><center>https://steemitimages.com/DQmTYoFePZJYVrnUv9KALNgxAHzozMkPqxY41Qw8A5z1ef6/c13.png</center></td>
</tr>
</table>

Notice that when the powers are odd integers, we have <strong>odd</strong> functions, and we have an <em>inflection point</em> at the origin (0,0). When the powers are even integers, we have <strong>even</strong> functions, and a <em>turning point</em> at the origin.

With the exception of <em>n</em> = 1, graphs with odd powers look like <em>x</em><sup>3</sup>, but they get progressively flatter when <em>x</em> is near 0. This is because for small values of <em>x</em>; <em>x</em><sup>3</sup>, <em>x</em><sup>5</sup> and so on, become smaller and smaller.

They get progressively steeper when |<em>x</em>| &ge; 1, because for larger values of <em>x</em>; <em>x</em><sup>3</sup>, <em>x</em><sup>5</sup> and so on, become larger and larger.

The same applies to even powers, except they look similar to <em>x</em><sup>2</sup> (a parabola).

The power functions of odd and even integers are overlaid on top of each other in Figures 1 and 2 respectively.

<table>
<tr>
<td><center>https://steemitimages.com/DQmTyipRhw5KDbdbZRbmRTUU799Jfp4F5upFGWFHgcpFYr9/c16.png<br/>Figure
 1. </center></td>
<td><center>https://steemitimages.com/DQmeDWgjeezLC8uPKBgm9tBsHe2cCu6NGKyAQ1jD5V38J6A/c19.png<br/>Figure 2.</center></td>
</tr>
</table>

Notice that for the odd powers, they have common intersection points at (-1,-1) and (1,1) and even powers (-1,1) and (1,1).

<hr/>

All equations in this tutorial were created with <a href="http://quicklatex.com/">QuickLatex</a>

All graphs are created with <a href="https://www.desmos.com/calculator">www.desmos.com/calculator</a>

<hr/>


Here's a list of posts created so far on the topic of Functions:

<ol>
<li><a href="https://steemit.com/steemiteducation/@masterwu/drawing-piecewise-defined-functions">Drawing piecewise defined functions</a></li>
<li><a href="https://steemit.com/steemiteducation/@masterwu/what-are-polynomial-functions">What are Polynomial Functions?</a></li>
<li>Power Functions: Case 1: a = n (n = 1,2,3...)</li>
</ol>

<hr/>

Please give me an <strong>Upvote</strong> and <strong>Resteem</strong> if you have found this tutorial helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3<br/>
Tip me at PayPal: https://paypal.me/MasterWu