create account

The Logistic Model for Population Growth by masterwu

View this thread on: hive.blog |  peakd.com |  ecency.com
steemiteducation · @masterwu · (edited)
$18.34
The Logistic Model for Population Growth
Here are some examples of "Logistic Growth" models used to predict the population of different organisms over time.

<center>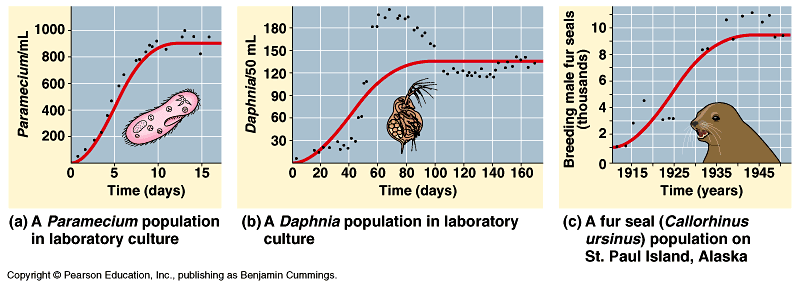![logisticpopns.gif](https://steemitimages.com/DQmS1R6zsmMuRza3vSTwaQ3nvJvWnFkkQZ6f64q3wpSoRQ3/logisticpopns.gif)</center>
<center><em><a href="http://www.bio.miami.edu/dana/pix/logisticpopns.gif">Image Source</a></em></center>

As you can see, according to this model, a population grows fast initially, but slows and approaches a certain "cap" called the carrying capacity.

We've seen in a <a href="https://steemit.com/steemiteducation/@masterwu/modelling-exponential-growth-of-bacteria-with-dy-dx-ky">previous post</a> that a basic model for population growth is the rate of population increase is proportional to the current population, or...

<center>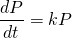![f1.png](https://steemitimages.com/DQmRpdR1uCaBMBKN75GJokBPS5Naz4Xu2NxPBxR1GuiW5cJ/f1.png)</center>

This differential equation describes exponential growth, where the growth rate dP/dt increases and the population P increases.

It might be a reasonable model if a species is given ideal growth conditions such as:

- Unlimited resources and space
- No predators
- Adequate nutrition
- Immunity from diseases

However, as we can clearly observe around us, no such conditions exist for any species, for if they did, it would be to the detriment of other species given the world's finite resources.

The exponential model of growth may be a good approximation initially, as displayed by bacterial cultures in a petri dish. However, the growth starts to slow and population levels off when it reaches a level that can no longer sustain an increasing growth rate.

We need a model that can approximate the declining rate of growth. What if we set up the differential equation as follows...

<center>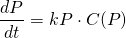![f2.png](https://steemitimages.com/DQmd42ZBB4TXEh5SMdZdqKRV3nLwFtV7UzMPQx3F99LEf1S/f2.png)</center>

...where C(P) is a coefficient that depends on the population P, such that:

<center>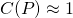![f3.png](https://steemitimages.com/DQmcSXXNKuRpFD2AHvKHa7rzmsdo2GhHtDxyx8pGN88uGaF/f3.png)</center>

...in the initial stages, when the population is low.

And in the later stages,

<center>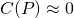![f4.png](https://steemitimages.com/DQmVZeYHQoZUYxou8qDA6nAde7CTjKgYRk8bwwVXadxBCvL/f4.png)</center>

...when population growth can no longer be sustained.

This way, in the beginning, the model for population growth in the early stages is an approximation of the exponential model...

<center>![f5.png](https://steemitimages.com/DQmTitSjhH5FpnVMRV12jpzdhhh41u19D7HdBZF9rLC4EbY/f5.png)</center>

And at a time when growth can no longer be sustained, the growth rate is...

<center>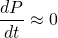![f6.png](https://steemitimages.com/DQmevKvyt62MDxwyu8zLr7FgRGtcwnzt41tcD2D1RRrUH6n/f6.png)</center>

Such a coefficient may be described by

<center>![f7.png](https://steemitimages.com/DQmNcBzU3XggZUHRNqJCLRDfAVaum6ZoRFTjaGFcwXNcUhb/f7.png)</center>

where <em>K</em> is called the carrying capacity for a given population - which is the maximum number that a species can be maintained at. As you can see, when <em>P</em> is low, at the beginning of growth, the ratio <em>P</em>/<em>K</em> is sufficiently small such that <em>C</em> is approximately equal to 1. When <em>P</em> is close to <em>K</em>, the ratio <em>P</em>/<em>K</em> is approximately equal to 1, so <em>C</em> approaches 0.

Let's call the function <em>C</em>(<em>P</em>) the "logistic coefficient". And thus we have the logistic equation...

<center>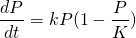![f8.png](https://steemitimages.com/DQmWtc4kv8R5VunfNCdu71Q8zrgRguJBkguYcGEQQYQqWmp/f8.png)</center>

...which was first published by Dutch mathematical biologist Pierre Verhulst around 1845. The logistic differential equation separable, and thus we can derive an explicit analytical solution.

So by rearranging and separating, we get...

<center>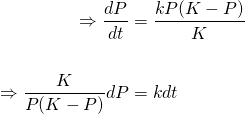![f9.png](https://steemitimages.com/DQmNdy3BHXmj49c9T3Gz76xWLUPGczwmS54i5eh6gkRUBuz/f9.png)</center>

On the left hand side, we can separate the term into partial fractions...

<center>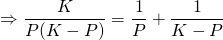![f10.png](https://steemitimages.com/DQmUmFVjjRJk1vEgc2RKBzWE8FeQ9CpfLotmJD8qgf85tjo/f10.png)</center>

And thus we can rewrite the differential equation and integrate both sides...

<center>![f11.png](https://steemitimages.com/DQmSbdoEygxS1LmVWsQ1qPCEBCtLPo2nXnjDP9UwKdS6MGS/f11.png)</center>

And thus we have derived the general solution for the logistic differential equation.

Ok, we'll leave it here for now. In the next tutorial, we will look at a specific example of applying the logistic equation to model the progressive growth of a population.

Below is a list of tutorials I've created so far on the subject of Differential Equations:

1. <a href="https://steemit.com/steemiteducation/@masterwu/introduction-to-differential-equations">Introduction to Differential Equations - Part 1</a>

2. <a href="https://steemit.com/steemiteducation/@masterwu/differential-equations-order-and-linearity">Differential Equations: Order and Linearity</a>

3. <a href="https://steemit.com/steemiteducation/@masterwu/first-order-differential-equations-with-separable-variables-example-1">First-Order Differential Equations with Separable Variables - Example 1</a>

4. <a href="https://steemit.com/steemiteducation/@masterwu/first-order-differential-equations-with-separable-variables-example-2">Separable Differential Equations - Example 2</a>

5. <a href="https://steemit.com/steemiteducation/@masterwu/modelling-exponential-growth-of-bacteria-with-dy-dx-ky">Modelling Exponential Growth of Bacteria with dy/dx = ky</a>

6. <a href="https://steemit.com/steemiteducation/@masterwu/modelling-the-decay-of-nuclear-medicine-with-dy-dx-ky">Modelling the Decay of Nuclear Medicine with dy/dx = -ky</a>

7. <a href="https://steemit.com/steemiteducation/@masterwu/modelling-the-discharge-of-a-capacitor-with-dy-dx-ky">Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky</a>

8. <a href="https://steemit.com/steemiteducation/@masterwu/mixing-salt-and-water-with-separable-differential-equations">Mixing Salt & Water with Separable Differential Equations</a>

9. <a href="https://steemit.com/steemiteducation/@masterwu/how-newton-s-law-of-cooling-cools-your-champagne">How Newton's Law of Cooling cools your Champagne</a>

10. The Logistic Model for Population Growth

Please give me an <strong>Upvote</strong> and <strong>Resteem</strong> if you have found this tutorial helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu
👍  , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , and 35 others
properties (23)
authormasterwu
permlinkthe-logistic-model-for-population-growth
categorysteemiteducation
json_metadata{"tags":["steemiteducation","steemstem","mathematics","calculus","teamaustralia"],"image":["https://steemitimages.com/DQmS1R6zsmMuRza3vSTwaQ3nvJvWnFkkQZ6f64q3wpSoRQ3/logisticpopns.gif","https://steemitimages.com/DQmRpdR1uCaBMBKN75GJokBPS5Naz4Xu2NxPBxR1GuiW5cJ/f1.png","https://steemitimages.com/DQmd42ZBB4TXEh5SMdZdqKRV3nLwFtV7UzMPQx3F99LEf1S/f2.png","https://steemitimages.com/DQmcSXXNKuRpFD2AHvKHa7rzmsdo2GhHtDxyx8pGN88uGaF/f3.png","https://steemitimages.com/DQmVZeYHQoZUYxou8qDA6nAde7CTjKgYRk8bwwVXadxBCvL/f4.png","https://steemitimages.com/DQmTitSjhH5FpnVMRV12jpzdhhh41u19D7HdBZF9rLC4EbY/f5.png","https://steemitimages.com/DQmevKvyt62MDxwyu8zLr7FgRGtcwnzt41tcD2D1RRrUH6n/f6.png","https://steemitimages.com/DQmNcBzU3XggZUHRNqJCLRDfAVaum6ZoRFTjaGFcwXNcUhb/f7.png","https://steemitimages.com/DQmWtc4kv8R5VunfNCdu71Q8zrgRguJBkguYcGEQQYQqWmp/f8.png","https://steemitimages.com/DQmNdy3BHXmj49c9T3Gz76xWLUPGczwmS54i5eh6gkRUBuz/f9.png","https://steemitimages.com/DQmUmFVjjRJk1vEgc2RKBzWE8FeQ9CpfLotmJD8qgf85tjo/f10.png","https://steemitimages.com/DQmSbdoEygxS1LmVWsQ1qPCEBCtLPo2nXnjDP9UwKdS6MGS/f11.png"],"links":["http://www.bio.miami.edu/dana/pix/logisticpopns.gif","https://steemit.com/steemiteducation/@masterwu/modelling-exponential-growth-of-bacteria-with-dy-dx-ky","https://steemit.com/steemiteducation/@masterwu/introduction-to-differential-equations","https://steemit.com/steemiteducation/@masterwu/differential-equations-order-and-linearity","https://steemit.com/steemiteducation/@masterwu/first-order-differential-equations-with-separable-variables-example-1","https://steemit.com/steemiteducation/@masterwu/first-order-differential-equations-with-separable-variables-example-2","https://steemit.com/steemiteducation/@masterwu/modelling-the-decay-of-nuclear-medicine-with-dy-dx-ky","https://steemit.com/steemiteducation/@masterwu/modelling-the-discharge-of-a-capacitor-with-dy-dx-ky","https://steemit.com/steemiteducation/@masterwu/mixing-salt-and-water-with-separable-differential-equations","https://steemit.com/steemiteducation/@masterwu/how-newton-s-law-of-cooling-cools-your-champagne","https://paypal.me/MasterWu"],"app":"steemit/0.1","format":"markdown"}
created2017-12-21 00:48:57
last_update2017-12-26 10:30:18
depth0
children6
last_payout2017-12-28 00:48:57
cashout_time1969-12-31 23:59:59
total_payout_value14.246 HBD
curator_payout_value4.097 HBD
pending_payout_value0.000 HBD
promoted0.000 HBD
body_length6,686
author_reputation6,368,408,965,910
root_title"The Logistic Model for Population Growth"
beneficiaries[]
max_accepted_payout1,000,000.000 HBD
percent_hbd10,000
post_id24,437,693
net_rshares2,955,809,352,883
author_curate_reward""
vote details (99)
@francesco.bonesi ·
$0.04
Very nice, thank you
👍  ,
properties (23)
authorfrancesco.bonesi
permlinkre-masterwu-the-logistic-model-for-population-growth-20171224t181720121z
categorysteemiteducation
json_metadata{"tags":["steemiteducation"],"app":"steemit/0.1"}
created2017-12-24 18:17:18
last_update2017-12-24 18:17:18
depth1
children1
last_payout2017-12-31 18:17:18
cashout_time1969-12-31 23:59:59
total_payout_value0.038 HBD
curator_payout_value0.002 HBD
pending_payout_value0.000 HBD
promoted0.000 HBD
body_length20
author_reputation160,833,553
root_title"The Logistic Model for Population Growth"
beneficiaries[]
max_accepted_payout1,000,000.000 HBD
percent_hbd10,000
post_id25,058,129
net_rshares7,851,384,439
author_curate_reward""
vote details (2)
@masterwu · 
Thanks for stopping by!
properties (22)
authormasterwu
permlinkre-francescobonesi-re-masterwu-the-logistic-model-for-population-growth-20171225t050857436z
categorysteemiteducation
json_metadata{"tags":["steemiteducation"],"app":"steemit/0.1"}
created2017-12-25 05:09:06
last_update2017-12-25 05:09:06
depth2
children0
last_payout2018-01-01 05:09:06
cashout_time1969-12-31 23:59:59
total_payout_value0.000 HBD
curator_payout_value0.000 HBD
pending_payout_value0.000 HBD
promoted0.000 HBD
body_length23
author_reputation6,368,408,965,910
root_title"The Logistic Model for Population Growth"
beneficiaries[]
max_accepted_payout1,000,000.000 HBD
percent_hbd10,000
post_id25,116,653
net_rshares0
@masterwu · 
@originalworks
properties (22)
authormasterwu
permlinkre-masterwu-the-logistic-model-for-population-growth-20171222t002716245z
categorysteemiteducation
json_metadata{"tags":["steemiteducation"],"users":["originalworks"],"app":"steemit/0.1"}
created2017-12-22 00:27:21
last_update2017-12-22 00:27:21
depth1
children1
last_payout2017-12-29 00:27:21
cashout_time1969-12-31 23:59:59
total_payout_value0.000 HBD
curator_payout_value0.000 HBD
pending_payout_value0.000 HBD
promoted0.000 HBD
body_length14
author_reputation6,368,408,965,910
root_title"The Logistic Model for Population Growth"
beneficiaries[]
max_accepted_payout1,000,000.000 HBD
percent_hbd10,000
post_id24,609,274
net_rshares0
@originalworks ·
$0.04
originalworks
The @OriginalWorks bot has determined this post by @masterwu to be original material and upvoted it! 
<center>![ezgif.com-resize.gif](https://steemitimages.com/DQmaBi37A5oTnQ9NBLH8YU4jpvhhmFauyvgg3YRrEJwskM9/ezgif.com-resize.gif)</center> 

To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
👍  
properties (23)
authororiginalworks
permlinkre-re-masterwu-the-logistic-model-for-population-growth-20171222t002716245z-20171222t003115
categorysteemiteducation
json_metadata"{"app": "pysteem/0.5.4"}"
created2017-12-22 00:31:15
last_update2017-12-22 00:31:15
depth2
children0
last_payout2017-12-29 00:31:15
cashout_time1969-12-31 23:59:59
total_payout_value0.028 HBD
curator_payout_value0.009 HBD
pending_payout_value0.000 HBD
promoted0.000 HBD
body_length344
author_reputation79,292,026,602,057
root_title"The Logistic Model for Population Growth"
beneficiaries[]
max_accepted_payout1,000,000.000 HBD
percent_hbd10,000
post_id24,609,660
net_rshares6,642,364,078
author_curate_reward""
vote details (1)
@mathfortress ·
$0.08
Great post on applications of differential equations. This is very useful in various fields such as ecology, biology, machine learning, chemistry, neural networks, medicine, physics and many more.
👍  ,
properties (23)
authormathfortress
permlinkre-masterwu-the-logistic-model-for-population-growth-20171222t172456855z
categorysteemiteducation
json_metadata{"tags":["steemiteducation"],"app":"steemit/0.1"}
created2017-12-22 17:25:03
last_update2017-12-22 17:25:03
depth1
children1
last_payout2017-12-29 17:25:03
cashout_time1969-12-31 23:59:59
total_payout_value0.062 HBD
curator_payout_value0.015 HBD
pending_payout_value0.000 HBD
promoted0.000 HBD
body_length196
author_reputation5,543,907,699,099
root_title"The Logistic Model for Population Growth"
beneficiaries[]
max_accepted_payout1,000,000.000 HBD
percent_hbd10,000
post_id24,729,194
net_rshares13,108,020,535
author_curate_reward""
vote details (2)
@masterwu · 
Thank you @mathfortress. Good to see another mathematician on Steemit!
properties (22)
authormasterwu
permlinkre-mathfortress-re-masterwu-the-logistic-model-for-population-growth-20171223t211302209z
categorysteemiteducation
json_metadata{"tags":["steemiteducation"],"users":["mathfortress"],"app":"steemit/0.1"}
created2017-12-23 21:13:12
last_update2017-12-23 21:13:12
depth2
children0
last_payout2017-12-30 21:13:12
cashout_time1969-12-31 23:59:59
total_payout_value0.000 HBD
curator_payout_value0.000 HBD
pending_payout_value0.000 HBD
promoted0.000 HBD
body_length70
author_reputation6,368,408,965,910
root_title"The Logistic Model for Population Growth"
beneficiaries[]
max_accepted_payout1,000,000.000 HBD
percent_hbd10,000
post_id24,918,437
net_rshares0
Help/Feedback