https://youtu.be/0pG6VJQ0UhU

In this video I go over a very interesting video on the concept of compound interest and show how at the end of the day, continuously compounded interest follows the Law of Natural Growth differential equation that I have covered many times in my earlier videos. Continuously compounded interest is when the interest is compounded instantaneously as opposed to, for example, annually or monthly. Compound interest is the concept of adding interest to a principle or initial amount of money periodically, and each time adding interest to the new sum. 

When we increase the frequency by which we compound the interest, the faster the rate of interest is built up. When we take this frequency and take the limit as it approaches an infinite amount of times, what we get is something very surprising: we obtain a formula that consists a limit that is in fact the very famous number e!! This is actually a truly remarkable finding, because we obtain the number e, as well as showing that it is the solution to the Law of Natural Growth differential equation, without any assumptions and strictly through the principles of compounded interest. This goes to show just how amazing mathematics is as many of the mathematical concepts developed by different people throughout many different generations all indeed are interconnected. This is a truly remarkable fact about mathematics, and this video perfectly illustrates that so make sure to watch this video!

---

Watch on DTube: https://d.tube/#!/v/mes/q2gl8we5
Watch on BitChute: https://www.bitchute.com/video/2E6yBZS8wJwJ/
Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIh6d9p-HSbTi8Y5rG6w

---

# View Video Notes Below!

---

>Download These Notes: Link is in Video Description.
>View These Notes as an Article: https://steemit.com/@mes
>Subscribe via Email: http://mes.fm/subscribe
>Donate! :) https://mes.fm/donate 
>
>Reuse of My Videos:
>- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
>
>Fight Back Against Censorship:
>- Bookmark sites/channels/accounts and check periodically
>- Remember to always archive website pages in case they get deleted/changed.
>
>Join my private Discord Chat Room: https://mes.fm/chatroom
>
>Check out my Reddit and Voat Math Forums:
>- Reddit: https://reddit.com/r/AMAZINGMathStuff
>- Voat: https://voat.co/v/AMAZINGMathStuff
>
>Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
>Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
>Watch my #AntiGravity Video Series: https://mes.fm/antigravity-playlist
>Follow My #MESExperiments Video Series: https://mes.fm/experiments-playlist>
>
>---
>
>NOTE: If you don't have time to watch this whole video:
>
>- Skip to the end for Summary and Conclusions (If Available)
>- Play this video at a faster speed.
>-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
>-- Try 4X+ Speed by Browser Extensions, HookTube.com, Modifying Source Code.
>-- **Browser Extension Recommendation: https://mes.fm/videospeed-extension**
>- Download and Read Notes.
>- Read notes on Steemit #GetOnSteem
>- Watch the video in parts.

---

# Differential Equations: Continuously Compounded Interest

If $1000 is invested at 6% interest, compounded annually, then:
	
- After 1 year the investment is worth: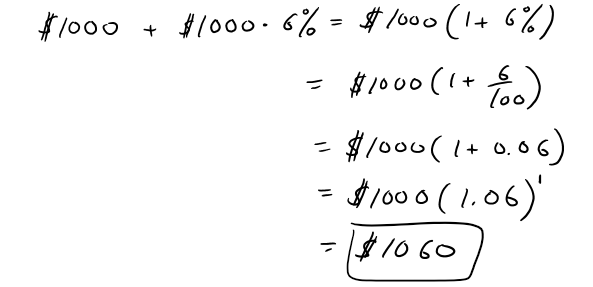

![](https://cdn.steemitimages.com/DQmNPv2yEoTjrPsiNeB9bm2oy2TbjeSaotvHr8xHm5HCN58/image.png)

- After 2 years the investment is worth: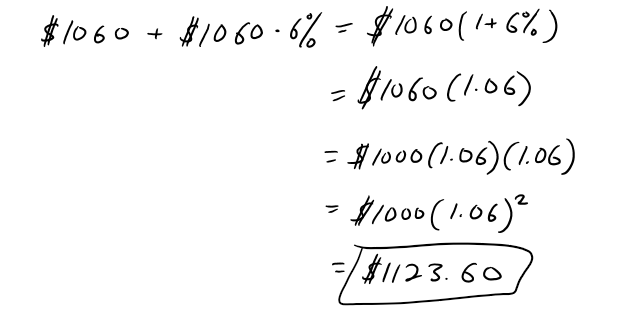

![](https://cdn.steemitimages.com/DQmeYZbpjUwFRcDcuJf7jPNNPv4As3pFZbVJSz4ZSjJc7SD/image.png)

- After t years the investment is worth: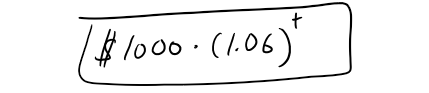

![](https://cdn.steemitimages.com/DQmYLo5KGrZBai3YpZ9Kjqx4nFWkLXuQdnJibKeX5BpBQzD/image.png)

In general, if an amount A<sub>0</sub> is invested at an interest rate r (r = 0.06 in this example), then after t years it's worth: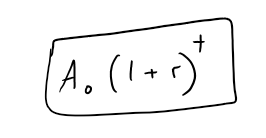

![](https://cdn.steemitimages.com/DQmQvdz3WWKDD3qeNoP265HqtzSwsv1NxAXbNnzE2tM4y3H/image.png)

Usually, however, interest is compounded more frequently, say n times a year.

Then in each compounding period the interest rate is r/n and there are nt compounding periods in t years, so the value of the investment is: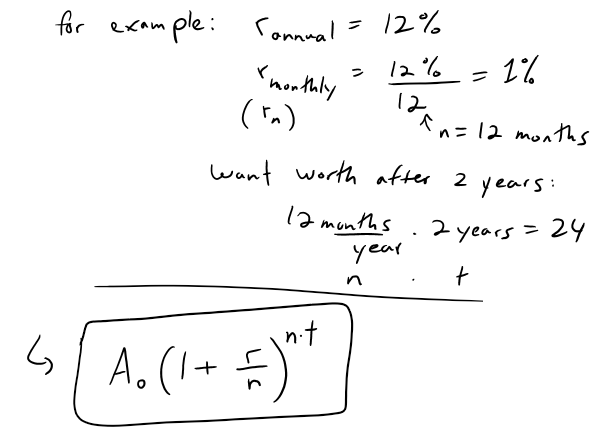 

![](https://cdn.steemitimages.com/DQmXo7VsxyGm3SMpDkLLgtGa8TZestDDaBbY3kUpg7QS1BE/image.png)

For instance, after 3 years at 6% interest a $1000 investment will be worth:

- Compounded Annually: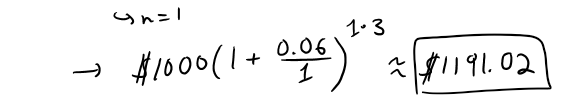

![](https://cdn.steemitimages.com/DQmZTP8KzSVXpkQ2FF6oZkp6NFxHoAzZM5Tg8ZYET16EvNd/image.png)

- Compounded Semiannually: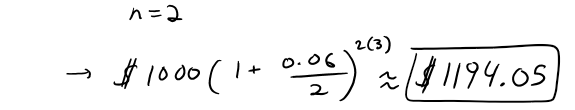

![](https://cdn.steemitimages.com/DQmfMkNWpJ9cNGRrSoAJ69HwYQBhQp6vC7VJmMVYb2AirQ7/image.png)

- Compounded Quarterly: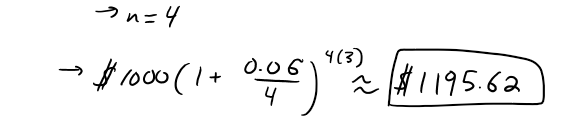

![](https://cdn.steemitimages.com/DQmQ1odBteWNTQqNH5SuQng19BtKmLWNKE8ogAYC4xF7Dww/image.png)

- Compounded Monthly: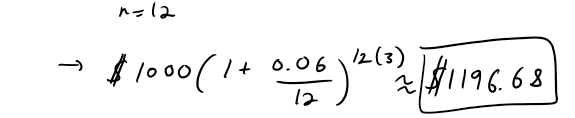

![](https://cdn.steemitimages.com/DQmdJrSWpYmEjhKBtbwRJHm2eTa4LwdQfDHpaKudBJA8hY7/image.png)

- Compounded Daily: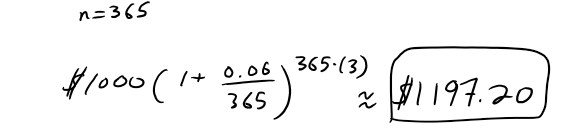

![](https://cdn.steemitimages.com/DQmSXBSdudrzLRWqGTz8Ve9mFbpZboxVpxQEnSeA46kVikb/image.png)

You can see that the interest paid increases as the number of compounding periods (n) increases.

If we let n → ∞, then we will be compounding the interest continuously and the value of the investment will be: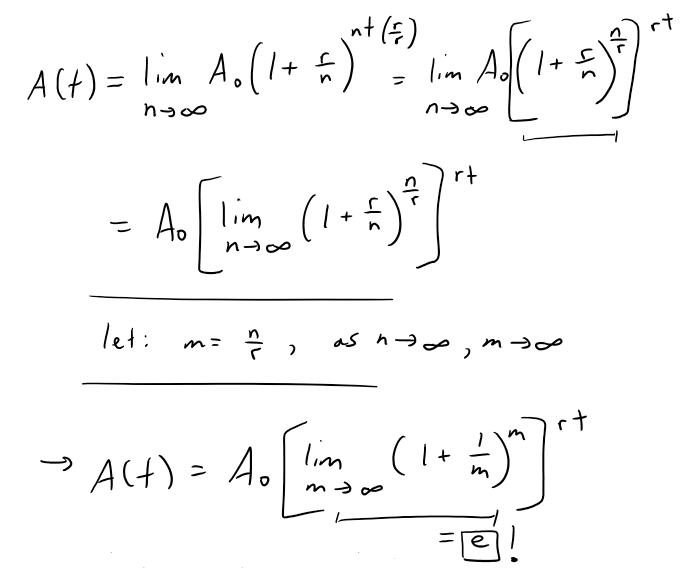

![](https://cdn.steemitimages.com/DQmNgKMpkTsBVy73sxVW9BWe3oMFLLHjptw5BSSPdKvSjRG/image.png)

But the limit in this expression is equal to the number e!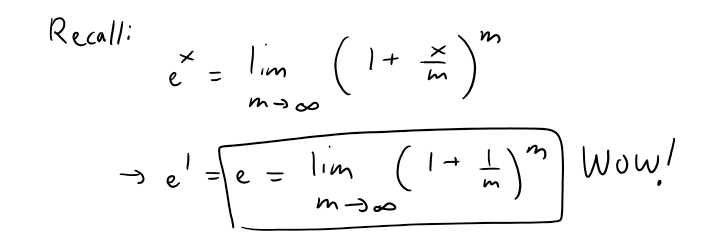

![](https://cdn.steemitimages.com/DQmT87zxeas1VvzNFGgvnXofXPMckk46jVknFZcp4RH4v6G/image.png)

So with continuous compounding of interest at interest rate r, the amount after t years is: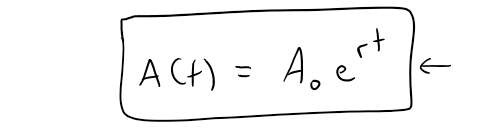

![](https://cdn.steemitimages.com/DQmPcM3cUjVy2LKjDWfYWufKMNo7vxFmwKrAB9iLofmt2dQ/image.png)

If we differentiate this equation, we get: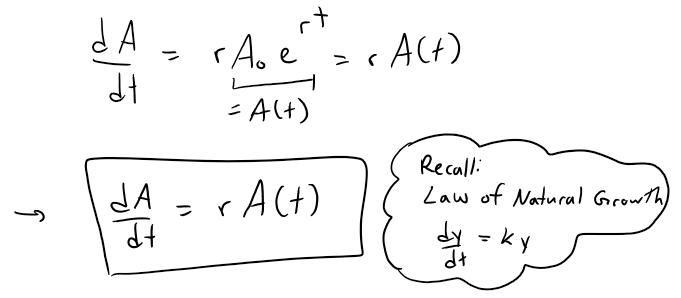 

![](https://cdn.steemitimages.com/DQmPTRvFD88gYRQ4S5yWteJy2YD8sT5ZEFmhKjpiy8yZwRL/image.png)

This equation says that, with continuous compounding of interest, the rate of increase of an investment is proportional to its size.

Returning to the example of $1000 invested for 3 years at 6% interest, we see that with continuous compounding of interest the value of the investment will be: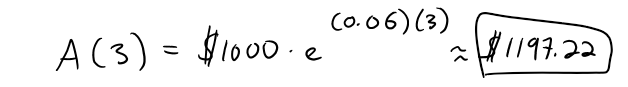

![](https://cdn.steemitimages.com/DQmZ7nUaob2JoMHsCbFtVsPwiZ7RCnCoqxroKCPUyKm2c4X/image.png)

Notice how close this is to the amount we calculated for daily compounding, $1197.20.

But the amount is easier to compute if we use continuous compounding.