In the section of [counting](https://steemit.com/mathematics/@sinbad989/a-gentle-introduction-to-mathematics-counting) we have determined the number k-subsets of a set of size n, denoted by 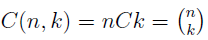 which is expressed in terms of binomial coefficients. **Binomial coefficient** is a powerful tool in mathematics. # Pascal’s Triangle <hr> Binomial coefficients can be arranged into a triangular array – known as Pascal’s triangle: <center>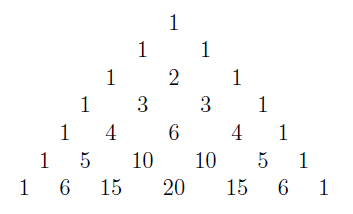</center> The power of this triangle is it can be used to calculate powers of binomials. ### Binomials A binomial is a polynomial with two terms. What if you want to determine the nth power of a binomial, for instance the 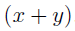. An example is to find the 6th power of 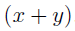 . We can start by finding the squared of 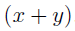 which is equal to 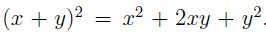 . From which, we can determine the cubed power, <center>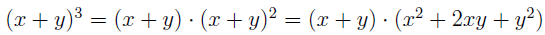</center> To determine the value of the last product we use the table method: <center>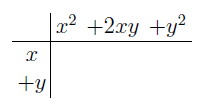</center> This gives us, <br> ![]<center>(https://steemitimages.com/DQmcgRLdNNGQypkX6fXjnCwaKsfRzR9QeAhrzJTiaMYGZmv/image.png)</center> Finally, we use this third power to determine the sixth power, thus <center>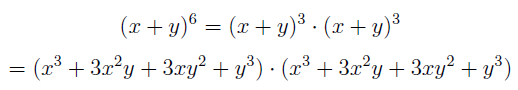</center> We can use table method again for the last product: <center>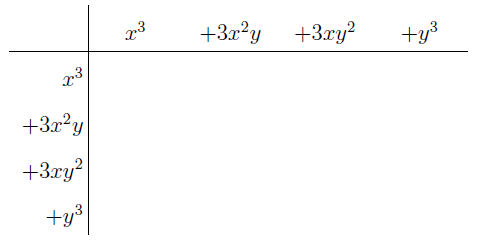</center> This will give us the final answer as: <center>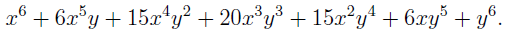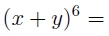</center> It took us a lot of work to reach this answer. Now, look at the answer above, the exponents on *x* starts at 6 and descends with each successive term down to 0. The same line of pattern holds for *y* but this time starting on the right side. Interestingly, the coefficients we have shown are actually the sixth row of the Pascal’s triangle. Fortunately, Pascal’s triangle is also easy to extend; that is, the number in the interior of the triangle is always the sum of the two above it. Consider the 7th and 8th row of the Pascal’s triangle: <center></center> With this tool, it becomes easier to determine the nth power of a binomial. <center>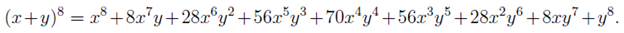</center> # Theorems regarding the Binomial Coefficients <hr> <center>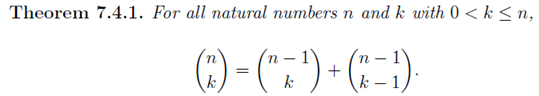</center> ### Proof 1: Combinatorial method The number of subsets of size *k* of the set 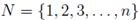 of size *n* is given by, 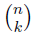 . We can partition these k-subsets into two disjoint cases: 1. Those that contain the final number n (set B) <br> 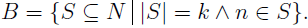 1. Those that does not contain the final number n (set A) <br> 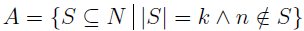 By addition rule, the size of the sum of the disjoint sets is given as, <center>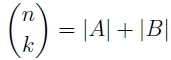</center> Set *A* is really just the set of all k-subsets of the (n-1)-set 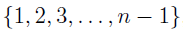 , thus the size of set A is defined to be, 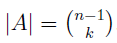 The set B can be obtained by adjoining the element n into a (k-1) subset of the (n-1)-set 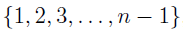 , thus the size of set B is given by, 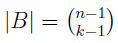 Substituting this values to the equation, <center>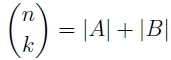</center> will give us, <center>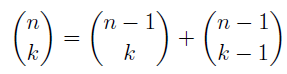</center> ### Proof 2: Algebraic method For the algebraic method, we will use the [two-column proof](https://steemit.com/mathematics/@sinbad989/a-gentle-introduction-to-mathematics-two-column-proof) so one can easily follow the arguments. | <center>Left-Side</center>| <center>Right-Side</center> | | -------- | -------- | | <center>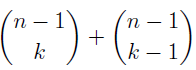 </center> | 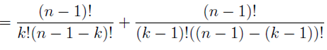 | | - | 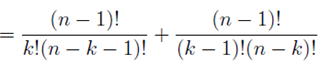 | | - | 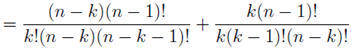 | | - | 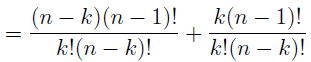 | | - | 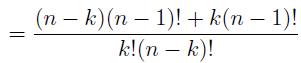 | |<center>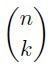 </center> |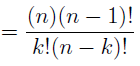 | <hr> <center>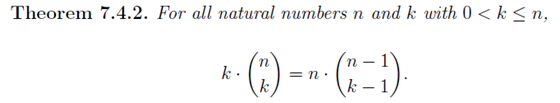 </center> ### Proof 1: Combinatorial method Consider a committee of *k* individuals one of whom has been chosen as chairperson. Similar kind of thinking can be applied to a collection of all subsets of size k taken from 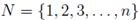, in which one of the elements is marked to distinguish it from the rest. We can count this collection in two ways: 1. We select a k-subset in 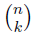 ways and then from among the k elements of the subset we could select one to be marked. This means, that there are 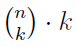 in our collection. 1. We could select an element in our n-set and consider it as the “marked” element of a subset. Then choose the additional k-1 elements from the remaining n-1 elements of the n-set. This implies that there are 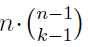 elements in our collection. Thus, <center>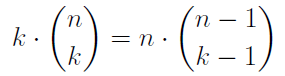</center> ### Proof 2: Algebraic method For the algebraic method, we will use the [two-column proof](https://steemit.com/mathematics/@sinbad989/a-gentle-introduction-to-mathematics-two-column-proof) so one can easily follow the arguments. | <center>Left-Side</center>| <center>Right-Side</center> | | -------- | -------- | | <center>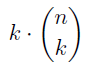 </center> | 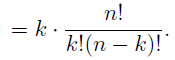 | | _ | 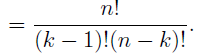 | | _ | 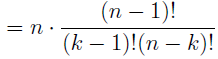 | | _ | 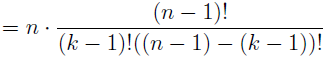 | | <center> 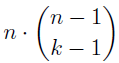 </center> | 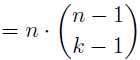 | <hr> <center> 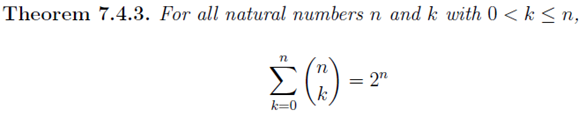 </center> ### Proof: The set of all subsets of 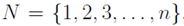 , which we denote as the power set of N 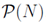, can be partitioned into n+1 sets based on the sizes of the subset. <center>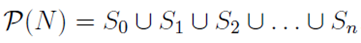</center> where 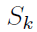 is a subset of the set N and that k is the size of the subset S, in symbolic form: <center>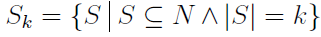</center> Two things to remember: 1. No subset of N can appear in two different parts of the partition (every 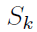 size is unique) 1. Every subset of N appears in one of the parts of the partition (sizes of subsets are all in the range from 0 to n). The addition principle tells us that the size of the power set is, <center>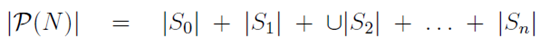</center> From previous [sections](https://steemit.com/mathematics/@sinbad989/a-gentle-introduction-to-mathematics-the-principle-of-mathematical-induction), we have shown that 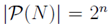, and we know that 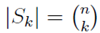, therefore <center>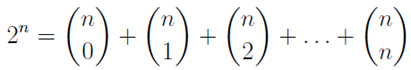</center> <hr> ### This will somehow serve as the summary of our story: <center>  </center> Substituting x=y=1 to Theorem 7.4.4, we have Theorem 7.4.3, <center> 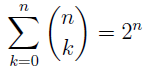 </center> Note that there is another proof without referring to the binomial theorem. This proof is **"like swatting a fly with a sledgehammer."** <br> <br> <sup>Disclaimer: this is a summary of section 7.4 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.</sup> 1. [A Gentle Introduction to the Art of Mathematics by Joe Field](https://github.com/valjen/book_collection) <hr> <center> Thank you for reading ...   </center>
| author | sinbad989 |
|---|---|
| permlink | a-gentle-introduction-to-mathematics-the-algebra-of-combinations |
| category | mathematics |
| json_metadata | {"tags":["mathematics","steemstem","steemiteducation","cebu","philippines"],"image":["https://steemitimages.com/DQmaKkDQLbbiokJ164ZqGsW3iuS1gW5kPJ9cprt8x6f2rRX/image.png","https://steemitimages.com/DQmUtB1jxuEk8dRexC29hLYovioYCQ3hrzmnmiFkFPGx6zs/image.png","https://steemitimages.com/DQmQ6qy9m5rfYbcq58S8rnCx2QU2RBP8t7FMv1uUTKdiFQ6/image.png","https://steemitimages.com/DQmSWqGj2CqZFq2rkdDoXoYepkmxSywnyy1JiA6D1HbZYno/image.png","https://steemitimages.com/DQmRhPuxfiRLwRWu9hEeaF2JiBziMmyfVPSMejVx96ip9WS/image.png","https://steemitimages.com/DQmW5ELebrzUuHb3XMScrjmFnDZhgL7gxULvgYsgzVvLgV7/image.png","https://steemitimages.com/DQmcgRLdNNGQypkX6fXjnCwaKsfRzR9QeAhrzJTiaMYGZmv/image.png","https://steemitimages.com/DQmehMD18i1o7pdVeiFnks5r8bAH3YW9LMaedfdtYGM21Qe/image.png","https://steemitimages.com/DQmNeTx6vro1m1XgE4N2tzEa2XzgiMdarDZurv9uqGki33f/image.png","https://steemitimages.com/DQmUqCfpns6mB4TMwXjf7fEyoyEjYFJPGVXimseA1wtTpYq/image.png","https://steemitimages.com/DQmYaxF4tCiGB2vPr5KRXqSB3MUNDwS3LtQvtMxumg82p88/image.png","https://steemitimages.com/DQmVi5PyrCWZ3R1gBwNkqA292bVUnJnWCvW5MPDeF3Em89m/image.png","https://steemitimages.com/DQmXXS6Mp3hRiSBGTW2dabJWLEVktCqPZqoB9k8hBUEwG4J/image.png","https://steemitimages.com/DQmWHyiySdkohbX243PqNNZoRTTcmo98SNR9y2AcRQGju1F/image.png","https://steemitimages.com/DQmTjLMfxmtd9inqbmem7hrBcuvRcGHj4AUWCdsc44evoYA/image.png","https://steemitimages.com/DQma8JEdJXgcTR4svcQzPVop5DfJa5tUwgwMrh9sQ8byPc2/image.png","https://steemitimages.com/DQmPcsEXjMXKZgtRwpjxt4yuuQA2vkCCP7zSd6CpwDt3wnf/image.png","https://steemitimages.com/DQmZT9vu8wveJ1K8SCY7JyKVqoQq5CjahiHCNGJyJrCB9fP/image.png","https://steemitimages.com/DQmRd2srn9Jtzc1CgZ6KW7QvgDoHsy9V5CLapEppcACC3af/image.png","https://steemitimages.com/DQmPyX3N4nGGNiktrTNqD9588DqMS8p8FN8twnn7oQpUy4p/image.png","https://steemitimages.com/DQmVFsEkxcdHPqgrTkFDrDw7UNZQtVB4xYeDkDSLDjbNzsH/image.png","https://steemitimages.com/DQmfTLPSFcSRmyRwkJ2HwQmN7yQ2x6vtGoeef18BvucZ6d3/image.png","https://steemitimages.com/DQmQWsdQNhQwFpa83VDYnHwoWck134vgHdgyc23yej6LFHf/image.png","https://steemitimages.com/DQmWSPeszSt9oYt81VrMqPuaUhgXiKa639UWMZF1NypZr1P/image.png","https://steemitimages.com/DQmdf2y6w9Bd3boyycMSA6CvFd9GE7UKWgdYZiX44u6HhHj/image.png","https://steemitimages.com/DQmSdjhmPJsYH8gd27bTrss4bZvFqVF7iiok4jmxmZpCtg2/image.png","https://steemitimages.com/DQmefotut9eayBwQwnHMh76FC996dsDsoeVSqpyjMhzWid3/image.png","https://steemitimages.com/DQmQDxDcEcRNmmLvCXBa47s3bn1CAjJfcq6YydqipZtszdP/image.png","https://steemitimages.com/DQmQHeSumXrBKDopRndYLzxvphLMyUAYmM27S7z8Xh5ZYXe/image.png","https://steemitimages.com/DQmNYTcWJk2NTz9ZA5MNkEwr8dQYky6Ky9aN5B232hFUKTg/image.png","https://steemitimages.com/DQmUb2QX6acJhbit8pYMHZH9xK2aQAvFq5pR8BKPabRJxns/image.png","https://steemitimages.com/DQme6XVvMDYBcKfYn7nCnjX52eH95K9V7mz5vZFjwmfTG8t/image.png","https://steemitimages.com/DQmSGe3v2uKmoP4imcLEzU43tchpAaWNyYpicDM5v8XMSq1/image.png","https://steemitimages.com/DQmVPQE2YeSBgkUEFA7Se88PzeqyPzKokKwZT7Eqw5ZwXBV/image.png","https://steemitimages.com/DQmd1TV3y8JhA48dpjQ1s1GwsCdjmYMV6NhNcQESzm8UM65/image.png","https://steemitimages.com/DQmWJCczDVs24NwkqgXnwP4BHWPkSNugYFhtbanFaER4aJ4/image.png","https://steemitimages.com/DQmU1FGvzyT1HzuZ7Hg8W6HfR4vQCeXdnXrG77JeZ6vYDFV/image.png","https://steemitimages.com/DQmYcd77ZSXJrcg19fdiTCAC4xxmsu1Vcfn53c5tgHyFjFD/image.png","https://steemitimages.com/DQma52wULRvRx5E9V6PcDR2QXug3ZfTRrXQ6CkpGnD3dLSi/image.png","https://steemitimages.com/DQmdg9RmQnvE5hzMWKc2ejdZ5LYEc3MPPyyL2iSZUv39hhf/image.png","https://steemitimages.com/DQmQmTWm8N7LcmzUM3Eyc3HiBVMHwtNXQFFgrtAJif8W834/image.png","https://steemitimages.com/DQmYfM2XGmNNhpkYeBJGFxngu9spfzn9bFCU8cu6mPG3PJg/image.png","https://steemitimages.com/DQmZaLJBkTb9vRHqvAQ3wUcdQT6Xvdho8p6QkKDJEcREyaB/image.png","https://steemitimages.com/DQmeUjbr4iFPgMdTssGdGhyY2ARagbapFfGjxz8Yi9nU3bK/image.png","https://steemitimages.com/DQmSuWsE6efdmcS9vBLFFjAjfBSENszzXLaXjm5CyRHpkeo/image.png","https://steemitimages.com/DQmaDE8eT34kRT1XMSti8D3agaVVaRqrj9fkrXURA6QiJhg/image.png","https://steemitimages.com/DQmYkVfRcCTbTxzE1AiPRNbZSpUgYn7a4nvgsZCc9tA5A7Y/image.png","https://steemitimages.com/DQmYjKjZKvC9Cw1s1VwQvqyKZn6t1q7KFBYZXsmSkDbF4Gs/image.png","https://steemitimages.com/DQmW8QC713KfUCTkfxpaSS998j4kPmXiCzxUbVkvdSAJ8i7/image.png","https://steemitimages.com/DQmNfm1BK8eGKpTHdmrXo8jDcuYaAKpgnBL4uaNManXd6Mm/image.png","https://steemitimages.com/DQmTjtwricPvBEnHVSaxGkxz22LHQEv377mTdMUo4USqQ94/image.png","https://steemitimages.com/DQmNyinkfEKtaRRsRhn7JqA7Sahfh7NHuK371ENZ68x6DYe/image.png","https://steemitimages.com/DQmcZ4wM2V2fFTYr5p8e8xwir4Pr3bNG8zcQvFPLZ6ssvSm/image.png","https://steemitimages.com/DQmPzNcoaHVtyWGnqp3aaC1uDv3SfjthhxtngKyYKSuqEQA/image.png","https://steemitimages.com/DQmfWLieGjcAAkK1rBHrXgmQyZiVbPsAeQugBuSV39rXxE4/image.png","https://steemitimages.com/DQmNXXLQdbXpB1WuRn2YErhQLznZVCdUW3kc7sutPWxA8vv/image.png"],"links":["https://steemit.com/mathematics/@sinbad989/a-gentle-introduction-to-mathematics-counting","https://steemit.com/mathematics/@sinbad989/a-gentle-introduction-to-mathematics-two-column-proof","https://steemit.com/mathematics/@sinbad989/a-gentle-introduction-to-mathematics-the-principle-of-mathematical-induction","https://github.com/valjen/book_collection"],"app":"steemit/0.1","format":"markdown"} |
| created | 2018-04-20 07:18:42 |
| last_update | 2018-04-20 07:18:42 |
| depth | 0 |
| children | 1 |
| last_payout | 2018-04-27 07:18:42 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.432 HBD |
| curator_payout_value | 0.125 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 11,432 |
| author_reputation | 1,082,780,746,128 |
| root_title | "A Gentle Introduction To Mathematics - The Algebra of Combinations" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 51,074,253 |
| net_rshares | 100,522,087,687 |
| author_curate_reward | "" |
| voter | weight | wgt% | rshares | pct | time |
|---|---|---|---|---|---|
| st3llar | 0 | 627,038,715 | 3% | ||
| bazhckovin | 0 | 57,137,038 | 100% | ||
| trest | 0 | 59,603,713 | 100% | ||
| zyta | 0 | 62,369,723 | 100% | ||
| sinbad989 | 0 | 1,216,107,494 | 100% | ||
| walljonathan | 0 | 410,007,960 | 100% | ||
| minnowvotes | 0 | 97,512,208,529 | 7.64% | ||
| natallia | 0 | 577,614,515 | 100% |
You got a 7.64% upvote from @minnowvotes courtesy of @sinbad989!
| author | minnowvotes |
|---|---|
| permlink | re-sinbad989-a-gentle-introduction-to-mathematics-the-algebra-of-combinations-20180420t082811683z |
| category | mathematics |
| json_metadata | {"app":"postpromoter/1.9.3"} |
| created | 2018-04-20 08:28:12 |
| last_update | 2018-04-20 08:28:12 |
| depth | 1 |
| children | 0 |
| last_payout | 2018-04-27 08:28:12 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 65 |
| author_reputation | -125,291,280,752 |
| root_title | "A Gentle Introduction To Mathematics - The Algebra of Combinations" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 51,083,358 |
| net_rshares | 0 |
 hiveblocks
hiveblocks