![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23yTjjyCiFkNhVwGBLBQUUGEr1ftmVPyNPt3VBZ4YxXwTYSoYfcfoGTdTvpPPkwSyzMiL.png)


---

*~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~*

---


**ENGLISH**
https://images.ecency.com/DQmNuqRpdWgTaWvjwbmaVWSemm13V7viV9jyRyVFHiMSbYA/optimized_image_1_.jpeg 

**24-06-2025 - Mathematical Analysis - Properties of functions [EN]-[IT]**
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-94)

***Properties of functions***

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/AK9NHqBrSBt5VzGGgou42kSKmJmJgaFvJzXrQ239HDBkj4UYPz4AbJc7BafSFbV.png)

*image created with artificial intelligence, the software used is Microsoft Copilot*

**The properties**
The main properties of functions are:
Domain
Sign
Parity
Periodicity
Continuity
Monotony
Relative extrema
Limits and asymptotes
Derivability

Below I briefly describe them some:

*Domain*
The domain is the set of values ​​of x for which the function is defined
Here is an example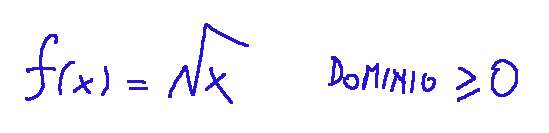

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23viTgJnyS3QJNMZ696WB2QQL9Fj4Z23HiYuvhsKENfvm9xnYU493dLvPeD1K5CFzKLRw.png)

*Sign*
The sign is basically the study of the function to see if it is positive, negative or zero.

*Parity*
Even is when the graph is symmetrical with respect to the y-axis
Odd is when the graph is symmetrical to the origin.

*Periodicity*
A function is said to be periodic when it repeats after a certain interval.
For example sin(x) has a period of 2π

**Analysis of a function**
*Example 1*
When we try to analyze a function we can discover its properties.
For example, take the following function: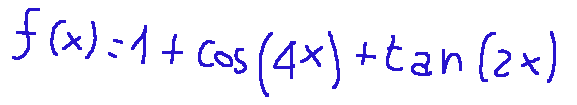

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/EonrnwUh4M14492F2R3ouZrDXmhLbeZJqvBn3XShnfmR9v41MiSbNit4NWtufpor4sJ.png)

We can say the following about this function.
It has a symmetry because we have cos, tan and 1 where:
cos(4x) is even
tan(2x) is odd
1 is a constant, therefore even.
We can also say that it has periodicity for the following reasons:
cos(4x) has period 2π/4 = π/2
tan(2x) has period = π/2
1 which is the constant does not influence.

We can therefore say that the function described above is **not symmetric and periodic with period π/2**

*Example 2*

Let's now take the following function as an example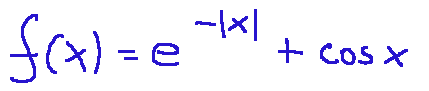

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23vsr8H9AZxioo4tCXG1xMrJVUWjvW8rpeemuTfwGfHWAQqcj7qSGB6wLzJ9wafMUq9aV.png)
as regards symmetry we can say that:
and raised to the minus absolute value of x is even
cos x is even
and the sum of two even functions is even

As regards periodicity we have that:
and raised to the minus absolute value of x is not periodic

So we can conclude that one of the properties that this function has is precisely that of being even.

**Even and Odd Graphs**
Below I show two graphs of two different functions. The graphs belong to two functions, one of which is called even and the other is called odd, so that the concept of even or odd function is visual as well as theoretical-written.

Example of a graph of an **even** function

The following graph corresponds to the function: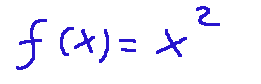

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/EoeMDuPzz8ZydKD7L3j4SKmxoUwHooaMHxve1y9zTB8H4rTXtz2KDyQ8cfb37fyT73W.png)

graph follows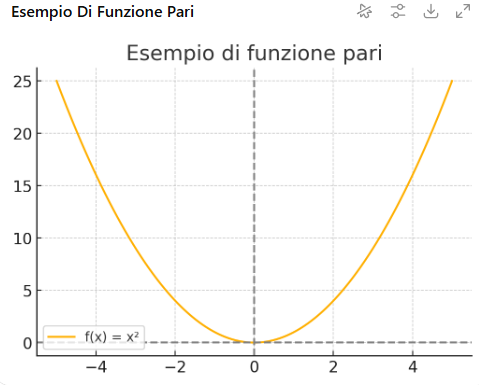

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23t8CfK4iu1pgC8bSBkA32J586aBVoZeCDNQNThhQXVcZVaHWhT66Zkr88ijiDowCvLnb.png)

*image created with artificial intelligence, the software used is Microsoft Copilot*

Example of a graph of an **odd** function

The following graph corresponds to the function: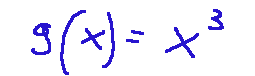

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23w3EiFMeHk7WmxsqUSNwfFr8CvAdoYz5PcS4u9uF2RuURBu5dY56YjMGJRGmxeyNgJan.png)

graph follows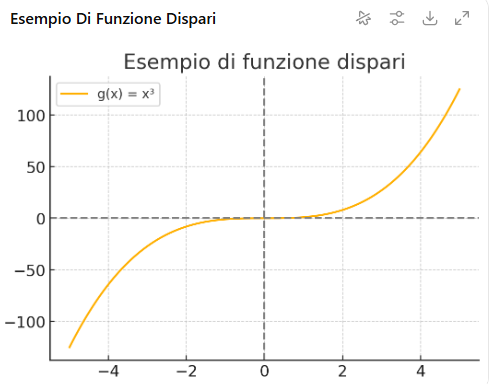

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23sxozwVD8pUxYE6o5RGACk6N9eCgHk4WPvhyYgVWnyZdXDNhmNhozKhpt8sATJBjfgaq.png)

*image created with artificial intelligence, the software used is Microsoft Copilot*

***Conclusions***
The properties of functions are important to understand how a phenomenon we are studying can vary.

***Question***
Did you know that the term function was introduced in 1968 by the German philosopher and mathematician Leibniz?




---

https://images.hive.blog/1536x0/https://files.peakd.com/file/peakd-hive/green77/gGQutTRs-hive-spacer.png

---


**ITALIAN**
https://images.ecency.com/DQmQ25zcp9Mna5r5gtLp786kVkVUpkVnQwgG7oWuMo88d7P/optimized_image.jpeg 

**24-06-2025 - Analisi Matematica - Proprietà delle funzioni [EN]-[IT]**
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-94)

***Proprietà delle funzioni***




![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/AK9NHqBrSBt5VzGGgou42kSKmJmJgaFvJzXrQ239HDBkj4UYPz4AbJc7BafSFbV.png)


*immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot*

**Le proprietà**
Le principali proprietà delle funzioni sono:
Dominio
Segno
Parità
Periodicità
Continuità
Monotonia
Estremi relativi
Limiti e asintoti
Derivabilità

Qui di seguito ne descrivo brevemente alcune:

*Dominio*
Il dominio è l'insieme dei valori di x per cui la funzione è definita
Qui di seguito un esempio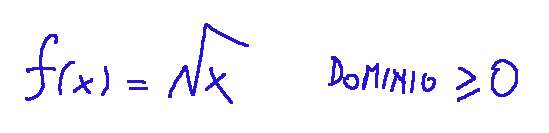

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23viTgJnyS3QJNMZ696WB2QQL9Fj4Z23HiYuvhsKENfvm9xnYU493dLvPeD1K5CFzKLRw.png)


*Segno*
Il segno praticamente è lo studio della funzione per vedere se è positiva, negativa o nulla.

*Parità*
Pari è quando il grafico è simmetrico rispetto all'asse y
Dispari è quando il grafico è simmetrico all'origine.

*Periodicità*
Si dice che una funzione è periodica quando si ripete dopo un certo intervallo.
Ad esempio sin(x) ha periodo di 2π

**Analisi di una funzione**
*Esempio 1*
QUando proviamo ad analizzare una funzione possiamo scoprirne le sue proprietà.
Ad esempio, prendiamo la seguente funzione: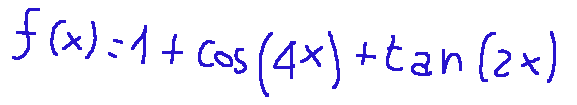

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/EonrnwUh4M14492F2R3ouZrDXmhLbeZJqvBn3XShnfmR9v41MiSbNit4NWtufpor4sJ.png)

Possiamo dire quanto segue di questa funzione.
Essa ha una simmetria in quanto abbiamo cos, tan e 1 dove:
cos(4x) è pari
tan(2x) è dispari
1 è una costante, quindi pari.
Possiamo dire anche che ha periodicità per i seguenti motivi:
cos(4x) ha periodo 2π/4 = π/2
tan(2x) ha periodo = π/2
1 che è la costante non influisce.

Possiamo quindi dire che la funzione descritta prima è **non simmetrica e periodica di periodo π/2**

*Esempio 2*

Prendiamo ora come esempio la seguente funzione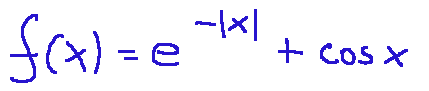

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23vsr8H9AZxioo4tCXG1xMrJVUWjvW8rpeemuTfwGfHWAQqcj7qSGB6wLzJ9wafMUq9aV.png)
per quanto riguarda la simmetria possiamo dire che:
e elevato a meno valore assoluto di x è pari
cos x è pari
e la somma di due funzioni pari è pari

Per quanto riguarda la periodicità abbiamo che:
e elevato a meno valore assoluto di x non è periodica

Quindi possiamo concludere che una delle proprietà che ha questa funzione è proprio quella di essere pari.

**Grafici pari e dispari**
Qui di seguito mostro due grafici di due funzioni diverse. I grafici appartengono a due funzioni, di cui una è denominata pari e l'altra è chiamata dispari, in modo che il concetto di funzione pari o dispari sia visivo oltre che teorico-scritto.

Esempio di un grafico di una funzione **pari**

Il grafico seguente corrisponde alla funzione: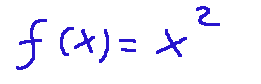


![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/EoeMDuPzz8ZydKD7L3j4SKmxoUwHooaMHxve1y9zTB8H4rTXtz2KDyQ8cfb37fyT73W.png)

segue grafico

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23t8CfK4iu1pgC8bSBkA32J586aBVoZeCDNQNThhQXVcZVaHWhT66Zkr88ijiDowCvLnb.png)

*immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot*



Esempio di un grafico di una funzione **dispari**

Il grafico seguente corrisponde alla funzione: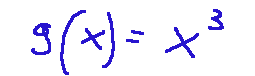

![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23w3EiFMeHk7WmxsqUSNwfFr8CvAdoYz5PcS4u9uF2RuURBu5dY56YjMGJRGmxeyNgJan.png)

segue grafico


![image.png](https://files.peakd.com/file/peakd-hive/stefano.massari/23sxozwVD8pUxYE6o5RGACk6N9eCgHk4WPvhyYgVWnyZdXDNhmNhozKhpt8sATJBjfgaq.png)

*immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot*




***Conclusioni***
Le proprietà delle funzioni sono importanti per comprendere come possa variare un fenomeno che stiamo studiando.

***Domanda***
Lo sapevate che il termine funzione fu introdotto nel 1968 dal filosofo e matematico tedesco Leibniz?


**THE END**