<div class="text-justify">
*little rant...*
If I were told that after undergraduate level, that I will still be faced with more complex mathematics (specifically statistics in this regard) at postgraduate level, I would not accept. What I thought I had finally escaped way back in university, was patiently waiting for me at higher level. As much as I could solve mathematical questions then, I still did not find it that interesting. The goal had always been to learn and pass it, that's all.
I could comfortably read and talk about medical stuffs, health and generally anything that is related with to biology, but not when it comes to calculations. I consider it only a want and not a need for me. However, it has turned out that practically, everything we do in one way or the other has mathematics.
What I am poised with now is theory of probability. I have been corrected countless times that theory of probability is not mathematics but rather statistics. I would not want to argue it anyway, what do I know. It is not my area of expertise, so I simply accept. I used to think that anything calculation is mathematics, I guess I was wrong. This course has so challenged me that I thought I knew nothing, not until I faced it squarely. With my the pseudo dedication and will to pass it, which of course I did well, along the line, it kind of became interesting because of the applicability of some of its theorems in solving complex real life problems.
<center>
[Jay Stewart and Monty Hall on the original version of the show let's make a deal](https://commons.wikimedia.org/wiki/File:Lets_make_a_deal_weekly_primetime.JPG)</center>
One of the most interesting question we were poised to solve as an assignment was a question named the **Monty Hall paradox**. I had practically no idea of what to do and where to start from, the only thing I observed was that the question looked like a question that probably the professor must have picked from one of the topic he taught - **Conditional probability**. So I decided to shoot my shot. Surprisingly, I got the mathematical answer but the entire ideology behind it was quite not clear then. However, that was an Eureka moment, haha. Alright, enough of my rant, let's talk about this problem in statistics.
*What is it about the Monty Hall paradox*
Commonly referred to as the Monty Hall problem was a game played on the television as a show and was hosted by the man named **Monty Hall** way back in 1963. The show was popularly called Let's make a deal, (LMAD). Usually there are 3 doors and behind two of them are goats and one has a car. For the player, their interest is in winning the game by choosing the one that has the car behind it.
To do this, the host simply allows the participant choose any door of their choice after which the host opens another door he knows that has goat behind it. The final stage is for the participant to decide if he or she will either decide to change their mind and pick the remaining door or retain their initial choice. If you are interested in the history, feel free to read it [here](https://en.wikipedia.org/wiki/Let%27s_Make_a_Deal) and also [here](https://encyclopediaofmath.org/wiki/Monty_hall_problem).
Our focus today in on understanding the ideology and the game itself and how you can use a conditional probability formula to solve the question. Fortunately, there are a lot of already written explanations to the paradox. However, it will not be out of place if I also share my approach.
Here goes the question:
>**Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2? "Is it to your advantage to switch your choice?**
I posted this same question on my whatsapp status to see how people will reason out the question, but to my greatest amazement, the responses were tilting towards retaining the original position. They believed that the host might be up to a shenanigan and at the long run may may cheat them out of them their prize. I laughed reading a lot of responses, and at that moment, I understood clearly that this question is highly paradoxical and intuitive.
Probably you are also thinking the same thing as them. Well, read on and we will find out soon enough if you will stick stick to your original choice or switch position. Probability is a random experiment (an experiment whose outcome is not known in advance and mostly subject to only chance). For example, when you role a dice or flip a coin, you possibly cannot predict the outcome of what will happen when the dice or coin lands. If the event happens, then it is assigned 1 and if it does not happen, then it is 0.
<center>
[Dice](https://commons.wikimedia.org/wiki/File:Dice_(11015609).jpg)</center>
The monty hall game also can be approached through classical probability method. In classical probability, the aim is to determine the likelihood or chance of the event occurring over the number of the total possible outcomes. Let's take the dice for example, we have a total of 6 (1, 2, 3, 4, 5, 6) possible outcome when we throw it. The chance of each number appearing is 1.
So if we want to calculate the probability of obtaining for example, say the number '4', then it is 1/6. Even if it is 5, it is still 1/6 and so on. This is so because all the number have equal chance of appearing. This is simply how classical probability operates and we will see its application later when we solve the Monty Hall question above.
Besides the classical approach, just like I informed you above, I personally applied another approach in probability - the **conditional probability**. Condition probability as the name implies, is the type of probability that measures the probability of an event occurring, given the fact that another event has already occurred.
<center>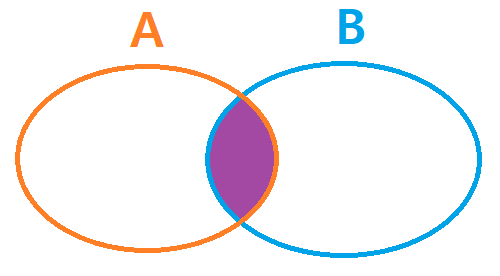
[Conditional Probability](https://commons.wikimedia.org/wiki/File:Conditional_probability.png)</center>
Similarly like the monty hall, the participant must first make a choice while the host opens the door. So to calculate the probability that the participant will win, knowing that there is already a car behind the door, using conditional probability just simply is also a right approach. Now you have an idea why I approached the monty hall question using this particular method. One event must happen for the other to happen.
*So is it wise to change your mind or not?*
By mere thinking without applying some principles, just relying on your instinct can actually make you make the wrong decision. As much as the experiment is still a probability, there are a still practical approaches that can increase your chances when you apply it. Your chances of winning in this case is more important, so how do we go about it?
<center>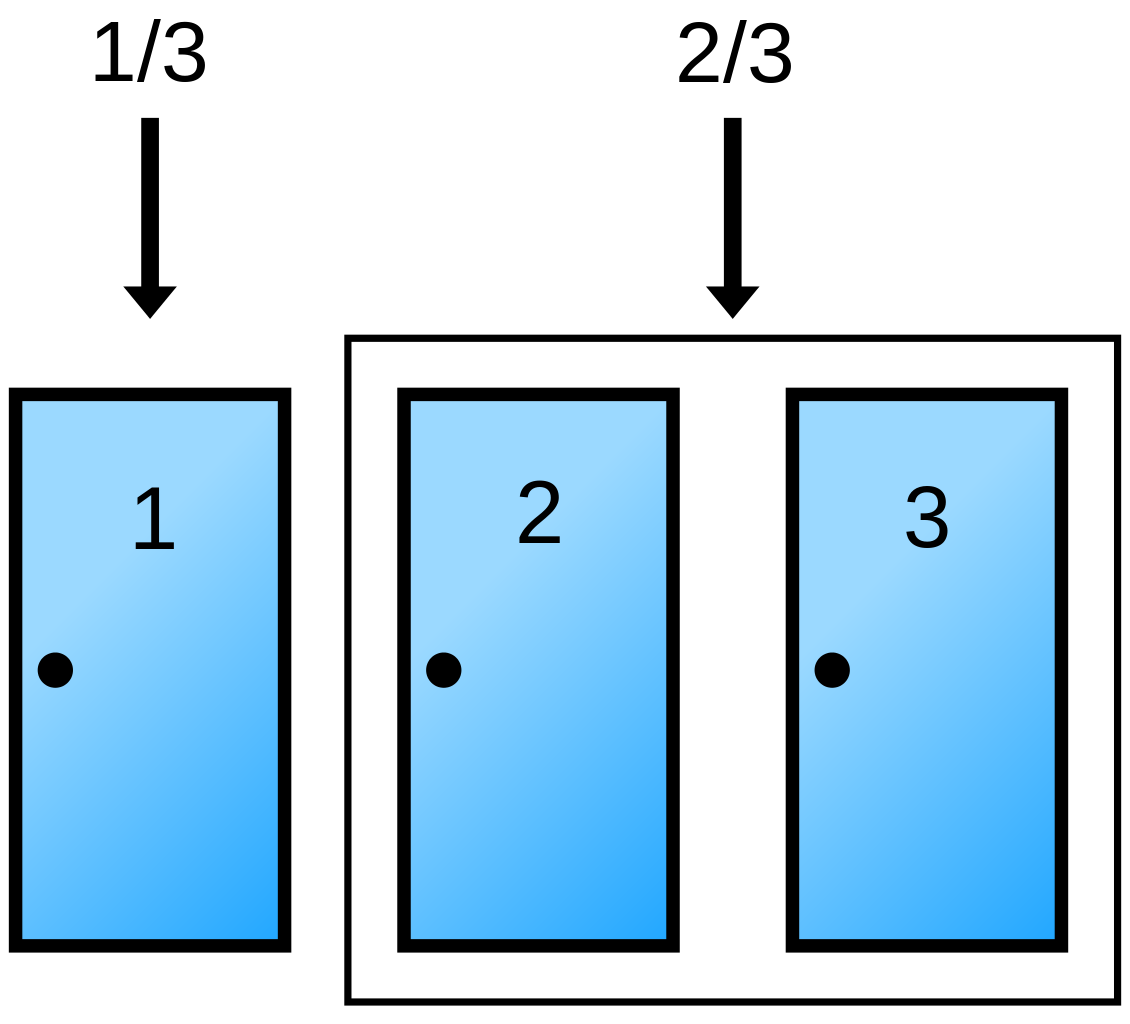
[Chances of winning in Monty Hall](https://commons.m.wikimedia.org/wiki/Monty_Hall_problem)</center>
Let's apply the classical approach. All things being equal, the chances of you wining the game is 1 out of 3 in all cases since you do not know behind which particular door lies the car. When you make a choice of a door, let's say door '1' without the host opening and asking you whether you want to change your mind, then the probability that you will win is 1/3 because this is the only chance that the car may be behind the door. Here, your chances of winning very low. Thus is depicted in the image above.
The remaining probability or chances that the car is behind the remaining two door is 2/3. Breaking this down, the car could also either be behind door 2 or door 3. By calculation you have {1/3 + 1/3} = 2/3. When the host who of course knows what is behind all the doors, decides to open any of the remaining two doors, for example door 3 and shows you a goat, the probability that the car will be behind the initial door '1' you have already selected did not change.
The host knows it all and will always reveal a goat no matter which door you choose. Therefore, if the car is behind door No. 1 and you chose that door, the host can choose to open either door No. 2 or door No. 3 to reveal a goat. However, if the car is behind door No. 2 or door No. 3 and you chose door No. 1, the host can only open the other door that has a goat behind it.
<center>
[Door 3 is exposed and happens to have goat behind it, hence this increases the chances of the car being behind the door '2'](https://commons.m.wikimedia.org/wiki/Monty_Hall_problem)</center>
So, what happens is that, the probability that the car will be behind door '2' only increased by 2/3, having in mind that the host has already opened the door '3'. This is more like increasing your chances of picking the right door as compared to when you chose the first door '1'.
<center>
[The moment of decision](https://commons.m.wikimedia.org/wiki/Monty_Hall_problem)</center>
Now you are left to decide, whether to go with the door that has 2/3 chances of win or sticking with your choice that has 1/3 chances of having the car behind it. Obviously, the best thing to do is to switch position since switching does increases your chances of picking the right door. The only situation in which you may loose is, if the car was actually behind the first door '1' you already chose, and this of course has lesser probability of occurrence when compared with door '2' with 2/3 probability.
Verdict: Switching does increases your chances of winning the game.
*Let's apply conditional probability*
This is more specifically the Bayes theorem. The major thing here is understanding the principle and then rightly applying the formula.
<center>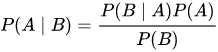
<sub>Bayes Theorem</sub></center>
Alright, let us approach it this way, based on the formula, we will also assign A, B, and C to the various events:
A = Event that the car is behind door A (door 1)
B = Event that the car is behind door B (door 2)
C = Event that the car is behind door C (door 3)
Just as we earlier explained above, the process here is almost the same, the major explanation probably needed here is to identify the conditional statements and to know how to apply it. Choosing door A, you have 1/3 chance that A has occurred while there will be a 2/3 chance that the remaining events B or C has occurred.
Once the host opens, say door C and shows you a goat, which he always do no matter the door you pick, it then means that C has occurred and the probability of this happening given that you have already selected the door A is 1/2 because the host always reveal a goat, constantly present.
Since we already know that the door C has a goat behind it, it means we are left to find the probability that the car might be behind door B given that we already know what is behind door C is goat, i.e. P[B|C], we have:
P[C] = Probability of the host showing a goat behind door C = **1/2**
P[B] = Prior probability of the car being behind door B = **1/3**.
P[C | B] = Probability of the host revealing a goat behind door C given that the car is behind door B = **1**. He will always show you a goat, hence a probability of occurrence.
In general, we will be having:
P[B|C] = P[C | B] x P[B] / P[C]
P[B|C] = 1 x 1/3 / 1/2 = 1/3 x 2/1 = 2/3
<center>
[Monty Hall Problem - Standard probabilities](https://commons.wikimedia.org/wiki/File:Monty_Hall_Problem_-_Standard_probabilities.svg)</center>
Therefore, the probability that the car might be behind door B given that we already know what is behind door C is goat, i.e. P[B|C] is equal to 2/3.
This clearly shows that switching puts you at an advantage of winning the game. This however does not imply that you will always win, but it gives you a better chance as when compared to you sticking to your initial choice.
The solution and approach to the monty hall problem actually has various approaches and tricks of solving it. As long as you understand the logic and apply the principle, you are most likely to arrive at the probability of 2/3 chances of the participant winning the game.
<sub>PS: I am not an expert in statistics nor mathematics, however, I have good understanding of some basic principles in theory of probability. Feel free to drop comment on any area you find confusing or not clear and we will address it together. We learn that way.</sub>
Alright, see ya.
**References**
<sub>[Understanding the Monty Hall Problem](https://betterexplained.com/articles/understanding-the-monty-hall-problem/)</sub>
<sub>[Why Humans Fail in Solving the Monty Hall Dilemma: A Systematic Review](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6194549/)</sub>
<sub>[Why You Should Always Switch: The Monty Hall Problem (Finally) Explained](https://behavioralscientist.org/steven-pinker-rationality-why-you-should-always-switch-the-monty-hall-problem-finally-explained/)</sub>
</div>| author | cyprianj | ||||||
|---|---|---|---|---|---|---|---|
| permlink | the-monthy-hall-paradox-a-clearer-understanding-of-the-game-the-idea-and-the-logic-behind-it | ||||||
| category | hive-196387 | ||||||
| json_metadata | {"app":"peakd/2023.2.2","format":"markdown","tags":["science","splinterlands","discovery-it","appreciator","neoxian","curangel","stemng","indiaunited","palnet","chessbrothers"],"users":[],"image":["https://files.peakd.com/file/peakd-hive/cyprianj/243gBKGuoL6zAhQ1zL67ikDkwojtoNwYNRLeNCEq3KqCPfpmLn7XMHd9p1MAqeRBU6BDD.png","https://files.peakd.com/file/peakd-hive/cyprianj/23xAVXZPnyAFBNe3pTZqUi4J3bYV51Sn6t8yFeGaASuEpk3PY4zaW9cCVkVQaJPUSjRXE.png","https://files.peakd.com/file/peakd-hive/cyprianj/23wCdf2Biq1YnA4VrfN1s1oJ9SD8WpDGxFuJSfV6UocYSYHfwKGsAP3SgmqmkYSLdDrxR.png","https://files.peakd.com/file/peakd-hive/cyprianj/23yT7Urwq9V1M5mF8LKK28tYvWTtP946hoMZ5DXohntjghY5SrAAbSpt2JxcmhZqi9vz9.png","https://files.peakd.com/file/peakd-hive/cyprianj/23wBbhCZzZy7TDmreihLD8iN3tugU6FjMuGSGwQfAfSLftY5cYP8MDuwPMh5djZwXb4yk.png","https://files.peakd.com/file/peakd-hive/cyprianj/23yJ3RrHL8N4cFWqJMAFuSi4kxKYU3kPs9iM2VH2SVtEc1Vd631PPntQPh8AUsjNSi5mM.png","https://files.peakd.com/file/peakd-hive/cyprianj/23swXQgUNzHCUaoqVQ7xJsMWUUjSApjCzgkGyzcvzGpiGuHbnAkuDqsV1mL1HSzFx4hUC.png","https://files.peakd.com/file/peakd-hive/cyprianj/AJmmqPhtEA3Hs83uE4RRSnGZuZUcitQ5frcwESXUCAcq78nW5RoKBzRumJA2aQ2.png"]} | ||||||
| created | 2023-02-25 20:49:54 | ||||||
| last_update | 2023-02-27 08:23:51 | ||||||
| depth | 0 | ||||||
| children | 9 | ||||||
| last_payout | 2023-03-04 20:49:54 | ||||||
| cashout_time | 1969-12-31 23:59:59 | ||||||
| total_payout_value | 9.402 HBD | ||||||
| curator_payout_value | 9.755 HBD | ||||||
| pending_payout_value | 0.000 HBD | ||||||
| promoted | 0.000 HBD | ||||||
| body_length | 14,015 | ||||||
| author_reputation | 75,398,556,172,423 | ||||||
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" | ||||||
| beneficiaries |
| ||||||
| max_accepted_payout | 1,000,000.000 HBD | ||||||
| percent_hbd | 10,000 | ||||||
| post_id | 121,121,061 | ||||||
| net_rshares | 34,835,701,802,531 | ||||||
| author_curate_reward | "" |
| voter | weight | wgt% | rshares | pct | time |
|---|---|---|---|---|---|
| xeldal | 0 | 7,890,975,655,902 | 14% | ||
| adol | 0 | 219,683,162,827 | 14% | ||
| enki | 0 | 2,753,964,841,483 | 14% | ||
| drifter1 | 0 | 988,274,629 | 2.8% | ||
| justtryme90 | 0 | 1,421,701,563 | 70% | ||
| eric-boucher | 0 | 14,136,172,712 | 2.8% | ||
| thecryptodrive | 0 | 38,823,670,355 | 1.12% | ||
| mammasitta | 0 | 12,117,684,928 | 2.8% | ||
| gerber | 0 | 2,498,370,956 | 3% | ||
| roelandp | 0 | 282,643,369,300 | 35% | ||
| daan | 0 | 51,064,336,773 | 8% | ||
| ezzy | 0 | 249,734,575 | 3% | ||
| cloh76 | 0 | 4,031,959,643 | 2.8% | ||
| nascimentoab | 0 | 993,578,553 | 2.8% | ||
| arcange | 0 | 976,932,159,116 | 5% | ||
| exyle | 0 | 16,231,498,783 | 3% | ||
| stea90 | 0 | 3,911,168,926 | 1% | ||
| joshglen | 0 | 732,054,459 | 5.6% | ||
| ace108 | 0 | 412,957,940,691 | 10% | ||
| pipokinha | 0 | 61,729,550,249 | 100% | ||
| akipponn | 0 | 3,208,691,739 | 35% | ||
| randomblock1 | 0 | 505,454,784 | 5.6% | ||
| lordvader | 0 | 54,997,543,680 | 5.6% | ||
| rmach | 0 | 12,882,103,499 | 35% | ||
| lemouth | 0 | 1,884,616,053,917 | 70% | ||
| alaqrab | 0 | 521,584,299 | 2.8% | ||
| lamouthe | 0 | 5,456,454,919 | 70% | ||
| tfeldman | 0 | 5,498,562,168 | 2.8% | ||
| metabs | 0 | 7,133,387,197 | 70% | ||
| mcsvi | 0 | 82,469,567,892 | 50% | ||
| lk666 | 0 | 1,842,911,372 | 2.8% | ||
| cnfund | 0 | 10,776,824,594 | 5.6% | ||
| justyy | 0 | 27,335,836,522 | 5.6% | ||
| michelle.gent | 0 | 3,259,967,095 | 1.12% | ||
| curie | 0 | 654,966,130,694 | 5.6% | ||
| modernzorker | 0 | 3,615,401,191 | 3.92% | ||
| techslut | 0 | 170,195,036,995 | 28% | ||
| steemstem | 0 | 4,035,274,411,997 | 70% | ||
| dashfit | 0 | 609,871,024 | 2.8% | ||
| tristancarax | 0 | 786,237,261 | 2.8% | ||
| edb | 0 | 8,753,726,928 | 7% | ||
| yadamaniart | 0 | 2,620,962,207 | 2.8% | ||
| apsu | 0 | 64,651,413 | 1.96% | ||
| bigtakosensei | 0 | 1,443,895,199 | 1.4% | ||
| walterjay | 0 | 485,501,391,744 | 35% | ||
| valth | 0 | 11,030,463,043 | 35% | ||
| metroair | 0 | 23,843,990,417 | 5.6% | ||
| driptorchpress | 0 | 1,917,728,142 | 1.4% | ||
| voter | 0 | 3,911,420,246 | 100% | ||
| sardrt | 0 | 1,237,057,024 | 10% | ||
| dna-replication | 0 | 2,715,940,766 | 70% | ||
| mariaalmeida | 0 | 16,813,920,833 | 100% | ||
| boynashruddin | 0 | 917,882,279 | 5.6% | ||
| torkot | 0 | 1,097,911,425 | 3.36% | ||
| gifmaster | 0 | 51,740,629,422 | 100% | ||
| steemiteducation | 0 | 2,871,782,668 | 2.8% | ||
| dhimmel | 0 | 387,513,929,935 | 17.5% | ||
| oluwatobiloba | 0 | 4,823,160,978 | 70% | ||
| detlev | 0 | 22,739,777,958 | 1.68% | ||
| chasmic-cosm | 0 | 851,533,844 | 2.8% | ||
| lizanomadsoul | 0 | 2,972,646,393 | 2% | ||
| lugaxker | 0 | 821,993,604 | 34.65% | ||
| federacion45 | 0 | 8,654,643,706 | 2.8% | ||
| amberyooper | 0 | 1,182,649,487 | 2.8% | ||
| gamersclassified | 0 | 3,149,330,510 | 2.8% | ||
| iansart | 0 | 9,327,753,242 | 2.8% | ||
| mvd | 0 | 1,148,942,319 | 2.8% | ||
| forykw | 0 | 5,459,615,046 | 1.5% | ||
| mobbs | 0 | 49,539,547,885 | 35% | ||
| jerrybanfield | 0 | 18,365,976,045 | 5.6% | ||
| roomservice | 0 | 1,058,230,231 | 2.8% | ||
| rt395 | 0 | 1,509,205,097 | 1.5% | ||
| bitrocker2020 | 0 | 10,718,029,058 | 0.84% | ||
| sustainablyyours | 0 | 31,426,778,015 | 35% | ||
| arunava | 0 | 7,891,478,750 | 0.56% | ||
| juancar347 | 0 | 17,734,529,695 | 3.36% | ||
| schoolforsdg4 | 0 | 1,049,274,145 | 5% | ||
| zerotoone | 0 | 1,123,369,029 | 2.8% | ||
| lorenzor | 0 | 1,297,421,960 | 50% | ||
| sam99 | 0 | 14,071,381,718 | 21% | ||
| aboutyourbiz | 0 | 1,037,884,014 | 5.6% | ||
| derosnec | 0 | 558,474,458 | 2.8% | ||
| alexander.alexis | 0 | 39,914,379,035 | 70% | ||
| dandesign86 | 0 | 15,180,585,233 | 8% | ||
| jayna | 0 | 6,865,855,827 | 1.12% | ||
| deanlogic | 0 | 1,394,044,141 | 2.8% | ||
| hhayweaver | 0 | 1,112,735,456 | 1.4% | ||
| princessmewmew | 0 | 7,482,168,291 | 2.8% | ||
| grapthar | 0 | 9,710,068,497 | 4.2% | ||
| imransoudagar | 0 | 94,691,033,152 | 100% | ||
| joeyarnoldvn | 0 | 486,671,901 | 1.47% | ||
| decomoescribir | 0 | 1,315,279,062 | 3.36% | ||
| diabolika | 0 | 754,960,340 | 2.8% | ||
| zacherybinx | 0 | 1,142,003,872 | 5.6% | ||
| zainalbakri | 0 | 521,965,145 | 1.68% | ||
| gunthertopp | 0 | 74,206,964,404 | 1.4% | ||
| pipiczech | 0 | 2,311,477,384 | 5.6% | ||
| binkyprod | 0 | 1,853,046,576 | 2.8% | ||
| empath | 0 | 4,074,746,730 | 2.8% | ||
| eturnerx | 0 | 94,710,261,968 | 5% | ||
| flatman | 0 | 5,082,794,920 | 5.6% | ||
| samest | 0 | 2,573,995,625 | 50% | ||
| analealsuarez | 0 | 1,204,242,688 | 35% | ||
| minnowbooster | 0 | 1,144,760,308,168 | 20% | ||
| felt.buzz | 0 | 12,932,980,214 | 1.4% | ||
| tsoldovieri | 0 | 7,330,357,974 | 35% | ||
| steemwizards | 0 | 4,076,204,153 | 5.6% | ||
| shitsignals | 0 | 965,982,165 | 3% | ||
| neumannsalva | 0 | 4,625,130,183 | 2.8% | ||
| stayoutoftherz | 0 | 139,841,348,564 | 1.4% | ||
| abigail-dantes | 0 | 25,688,097,964 | 70% | ||
| coindevil | 0 | 2,786,744,648 | 4.48% | ||
| bambukah | 0 | 908,550,563 | 4% | ||
| zonguin | 0 | 4,638,087,018 | 17.5% | ||
| prapanth | 0 | 1,195,632,237 | 2.8% | ||
| martibis | 0 | 2,495,766,886 | 1.68% | ||
| val.halla | 0 | 2,869,753,262 | 10% | ||
| redrica | 0 | 1,920,505,560 | 2.8% | ||
| pepskaram | 0 | 594,251,943 | 2.8% | ||
| iamphysical | 0 | 18,564,728,612 | 90% | ||
| dipom98 | 0 | 1,180,156,057 | 2.8% | ||
| zest | 0 | 1,003,920,540 | 35% | ||
| zyx066 | 0 | 4,757,269,359 | 1.68% | ||
| chrisdavidphoto | 0 | 1,062,303,396 | 1.68% | ||
| revo | 0 | 10,832,829,280 | 5.6% | ||
| felander | 0 | 12,623,472,219 | 3% | ||
| azulear | 0 | 995,385,064 | 100% | ||
| psicoluigi | 0 | 736,309,736 | 50% | ||
| nerdnews | 0 | 983,566,064 | 5.6% | ||
| wilians | 0 | 548,137,818 | 35% | ||
| rocky1 | 0 | 781,291,378,804 | 0.84% | ||
| stickchumpion | 0 | 609,459,831 | 2.8% | ||
| noloafing | 0 | 728,983,087 | 17.5% | ||
| massivevibration | 0 | 25,198,837,730 | 30% | ||
| adi.pisces | 0 | 579,086,981 | 1.68% | ||
| vera-vaders-ea | 0 | 507,314,742 | 5.6% | ||
| accelerator | 0 | 45,809,225,635 | 60% | ||
| raj808 | 0 | 1,942,127,187 | 1.68% | ||
| aidefr | 0 | 7,342,367,337 | 35% | ||
| torico | 0 | 1,474,034,472 | 1.84% | ||
| cloudspyder | 0 | 8,582,570,341 | 100% | ||
| yogacoach | 0 | 631,825,791 | 3% | ||
| sorin.cristescu | 0 | 10,836,086,014 | 2.8% | ||
| procryptix | 0 | 32,972,492,575 | 100% | ||
| therealwolf | 0 | 33,715,769,742 | 2.8% | ||
| fatman | 0 | 8,716,486,618 | 2% | ||
| inthenow | 0 | 22,960,224,990 | 25% | ||
| minnowpowerup | 0 | 873,714,184 | 2.8% | ||
| cryptononymous | 0 | 1,913,483,594 | 2.8% | ||
| upme | 0 | 1,771,558,196 | 2.8% | ||
| dauerossi | 0 | 5,884,570,693 | 30% | ||
| meno | 0 | 21,296,094,360 | 2.8% | ||
| bigdizzle91 | 0 | 767,970,694 | 2.8% | ||
| steemed-proxy | 0 | 1,024,926,348,897 | 5.6% | ||
| fatkat | 0 | 1,467,891,849 | 2.79% | ||
| investegg | 0 | 15,188,054,046 | 19.9% | ||
| peaceandwar | 0 | 881,593,823 | 2.8% | ||
| bhoa | 0 | 3,630,830,978 | 35% | ||
| enzor | 0 | 2,132,709,881 | 35% | ||
| marcoriccardi | 0 | 1,034,435,648 | 5.6% | ||
| bartosz546 | 0 | 2,896,731,747 | 2.8% | ||
| tazbaz | 0 | 555,528,130 | 2.8% | ||
| dreamm | 0 | 2,962,496,981 | 50% | ||
| dandays | 0 | 16,371,176,533 | 1.96% | ||
| battebilly | 0 | 800,592,089 | 2.8% | ||
| notb4mycoffee | 0 | 3,202,896,635 | 5.6% | ||
| silverwhale | 0 | 1,451,651,328 | 5.04% | ||
| dejan.vuckovic | 0 | 636,255,017 | 2.8% | ||
| alvinauh | 0 | 1,284,189,231 | 30% | ||
| lottje | 0 | 612,414,932 | 70% | ||
| myach | 0 | 899,551,154 | 4.48% | ||
| sunsea | 0 | 4,159,418,338 | 2.8% | ||
| omstavan | 0 | 7,001,468,506 | 100% | ||
| bluefinstudios | 0 | 3,533,315,057 | 1.68% | ||
| steveconnor | 0 | 4,731,249,617 | 2.8% | ||
| sankysanket18 | 0 | 1,652,708,070 | 35% | ||
| dbddv01 | 0 | 2,544,279,312 | 17.5% | ||
| zmx | 0 | 555,782,642 | 2.8% | ||
| nicole-st | 0 | 16,566,755,468 | 2.8% | ||
| smartsteem | 0 | 138,318,293,370 | 2.8% | ||
| fredkese | 0 | 594,738,938 | 5% | ||
| aboutcoolscience | 0 | 68,097,827,380 | 70% | ||
| afifa | 0 | 590,902,030 | 10% | ||
| skycae | 0 | 732,834,535 | 5.6% | ||
| sgt-dan | 0 | 27,036,350,469 | 50% | ||
| cahlen | 0 | 802,307,603 | 1.4% | ||
| xanderslee | 0 | 506,255,472 | 5.6% | ||
| kenadis | 0 | 18,750,778,962 | 70% | ||
| bebeomega | 0 | 1,256,572,281 | 2.8% | ||
| robotics101 | 0 | 20,256,668,634 | 70% | ||
| marcolino76 | 0 | 566,228,346 | 2.8% | ||
| onemedia | 0 | 1,129,713,846 | 5.6% | ||
| lpv | 0 | 2,890,914,042 | 8.75% | ||
| punchline | 0 | 15,370,974,253 | 5.6% | ||
| howiemac | 0 | 627,925,908 | 2.8% | ||
| gentleshaid | 0 | 15,092,216,702 | 100% | ||
| stevenson7 | 0 | 598,861,977 | 2.8% | ||
| apon318 | 0 | 490,860,948 | 5.6% | ||
| tomatom | 0 | 636,585,195 | 2.8% | ||
| duke77 | 0 | 7,033,946,365 | 33% | ||
| danaedwards | 0 | 750,426,042 | 5.6% | ||
| r00sj3 | 0 | 134,477,244,976 | 35% | ||
| sco | 0 | 18,549,605,400 | 70% | ||
| anikekirsten | 0 | 3,086,471,902 | 35% | ||
| phgnomo | 0 | 812,781,642 | 2.8% | ||
| ennyta | 0 | 914,776,907 | 50% | ||
| gordon92 | 0 | 848,051,234 | 2.8% | ||
| stahlberg | 0 | 1,290,047,478 | 2.8% | ||
| gabrielatravels | 0 | 1,045,152,689 | 1.96% | ||
| cordeta | 0 | 1,018,764,368 | 5.6% | ||
| reizak | 0 | 498,030,165 | 2.24% | ||
| vjap55 | 0 | 3,364,890,968 | 100% | ||
| carn | 0 | 3,489,044,934 | 5.04% | ||
| branbello | 0 | 2,677,064,119 | 35% | ||
| bartheek | 0 | 2,140,852,838 | 5.6% | ||
| hetty-rowan | 0 | 523,571,664 | 2.8% | ||
| ydavgonzalez | 0 | 3,634,940,666 | 10% | ||
| intrepidphotos | 0 | 1,275,054,609,390 | 52.5% | ||
| itwithsm | 0 | 4,717,185,051 | 100% | ||
| fineartnow | 0 | 3,828,522,757 | 2.8% | ||
| oscarina | 0 | 726,424,704 | 10% | ||
| bengy | 0 | 3,510,741,575 | 3% | ||
| yoghurt | 0 | 2,771,822,880 | 5.6% | ||
| shinedojo | 0 | 719,344,404 | 5.6% | ||
| fragmentarion | 0 | 18,280,281,323 | 70% | ||
| bennettitalia | 0 | 1,060,147,518 | 2.8% | ||
| jigstrike | 0 | 881,990,310 | 2.8% | ||
| baycan | 0 | 966,920,217 | 2.8% | ||
| aakom | 0 | 489,904,534 | 100% | ||
| dynamicrypto | 0 | 799,942,629 | 1% | ||
| sawko | 0 | 1,108,233,046 | 100% | ||
| neneandy | 0 | 6,485,040,901 | 5.6% | ||
| pab.ink | 0 | 45,466,563,922 | 35% | ||
| jnmarteau | 0 | 552,512,319 | 2% | ||
| real2josh | 0 | 661,181,182 | 35% | ||
| soufiani | 0 | 2,340,906,112 | 2.24% | ||
| gribouille | 0 | 736,095,991 | 16.5% | ||
| itharagaian | 0 | 3,786,647,359 | 33% | ||
| cool08 | 0 | 619,534,830 | 2.8% | ||
| stemng | 0 | 9,902,553,280 | 100% | ||
| grizzle | 0 | 1,286,052,634 | 2.8% | ||
| kingabesh | 0 | 2,033,173,543 | 50% | ||
| miguelangel2801 | 0 | 761,141,644 | 50% | ||
| mproxima | 0 | 1,961,167,090 | 2.8% | ||
| didic | 0 | 1,940,579,127 | 2.8% | ||
| warpedpoetic | 0 | 1,793,292,445 | 5.6% | ||
| orlandumike | 0 | 19,142,509,960 | 20% | ||
| careassaktart | 0 | 1,136,956,652 | 1.68% | ||
| dexterdev | 0 | 2,882,479,770 | 35% | ||
| nwjordan | 0 | 862,835,978 | 5.6% | ||
| themonkeyzuelans | 0 | 1,062,401,319 | 2.8% | ||
| florenceboens | 0 | 3,968,691,679 | 10% | ||
| zelenicic | 0 | 30,650,267,198 | 100% | ||
| geopolis | 0 | 4,636,336,120 | 70% | ||
| ajfernandez | 0 | 770,832,952 | 100% | ||
| robertbira | 0 | 7,583,457,039 | 17.5% | ||
| the.chiomz | 0 | 1,107,162,984 | 55% | ||
| lebastion | 0 | 1,119,709,661 | 33% | ||
| alexdory | 0 | 10,682,768,554 | 70% | ||
| sargewhale | 0 | 838,237,184 | 100% | ||
| irgendwo | 0 | 18,234,041,968 | 5.6% | ||
| vegan.niinja | 0 | 493,767,308 | 2.8% | ||
| flugschwein | 0 | 3,666,875,078 | 59.5% | ||
| cyprianj | 0 | 27,903,853,527 | 50% | ||
| kieranstone | 0 | 1,508,988,834 | 1.84% | ||
| melvin7 | 0 | 22,898,253,953 | 35% | ||
| francostem | 0 | 9,655,670,211 | 70% | ||
| endopediatria | 0 | 686,093,171 | 20% | ||
| technologix | 0 | 3,679,067,256 | 5.6% | ||
| chrislybear | 0 | 14,680,306,333 | 50% | ||
| jjerryhan | 0 | 2,056,323,333 | 2.8% | ||
| cryptictruth | 0 | 1,797,884,817 | 0.5% | ||
| zipporah | 0 | 2,754,096,232 | 1.12% | ||
| leomarylm | 0 | 1,408,092,166 | 2.8% | ||
| randumb | 0 | 710,969,533 | 5.6% | ||
| djoi | 0 | 2,004,434,580 | 50% | ||
| positiveninja | 0 | 1,103,873,579 | 2.8% | ||
| miroslavrc | 0 | 924,531,556 | 1.4% | ||
| foxyspirit | 0 | 549,310,984 | 2.8% | ||
| bscrypto | 0 | 13,770,071,298 | 2.8% | ||
| vonaurolacu | 0 | 1,679,643,967 | 2.8% | ||
| movingman | 0 | 1,223,508,319 | 20% | ||
| delpilar | 0 | 934,959,443 | 25% | ||
| proto26 | 0 | 2,549,772,753 | 5.6% | ||
| tomastonyperez | 0 | 16,394,344,617 | 50% | ||
| rodrigocassio | 0 | 893,205,438 | 100% | ||
| bil.prag | 0 | 2,057,806,928 | 0.28% | ||
| silviomangum29 | 0 | 893,174,523 | 100% | ||
| elvigia | 0 | 10,699,561,544 | 50% | ||
| bestboom | 0 | 517,274,797 | 3% | ||
| viagens | 0 | 895,593,251 | 100% | ||
| vittoriozuccala | 0 | 2,191,765,914 | 2.8% | ||
| laxam | 0 | 5,220,772,273 | 100% | ||
| koenau | 0 | 1,513,238,518 | 2.8% | ||
| qberry | 0 | 3,772,161,531 | 2.8% | ||
| strosalia | 0 | 10,529,932,492 | 80% | ||
| frissonsteemit | 0 | 1,235,563,844 | 2.8% | ||
| broncofan99 | 0 | 8,104,820,723 | 20% | ||
| rambutan.art | 0 | 1,537,517,690 | 5.6% | ||
| greddyforce | 0 | 4,290,735,775 | 2.07% | ||
| flyerchen | 0 | 638,499,537 | 2.8% | ||
| albus.draco | 0 | 1,116,300,004 | 33% | ||
| braaiboy | 0 | 13,282,553,591 | 2.8% | ||
| sd974201 | 0 | 1,397,104,128 | 3% | ||
| gadrian | 0 | 310,735,536,135 | 52.5% | ||
| c0wtschpotato | 0 | 583,438,104 | 2.8% | ||
| fotogruppemunich | 0 | 3,003,783,786 | 1.4% | ||
| therising | 0 | 97,801,858,789 | 5.6% | ||
| cryptocoinkb | 0 | 2,155,987,719 | 2.8% | ||
| scruffy23 | 0 | 20,004,712,037 | 50% | ||
| eniolw | 0 | 4,894,649,793 | 100% | ||
| de-stem | 0 | 38,280,090,424 | 69.3% | ||
| imcore | 0 | 874,616,596 | 10% | ||
| serylt | 0 | 3,230,059,417 | 68.6% | ||
| misterlangdon | 0 | 1,222,459,384 | 50% | ||
| lilacse | 0 | 23,401,851,963 | 100% | ||
| josedelacruz | 0 | 4,512,751,679 | 50% | ||
| achimmertens | 0 | 6,129,234,443 | 2.8% | ||
| lorenzopistolesi | 0 | 10,110,535,528 | 2.8% | ||
| oscurity | 0 | 746,588,478 | 0.7% | ||
| mariusfebruary | 0 | 729,748,388 | 2.24% | ||
| outtheshellvlog | 0 | 875,170,106 | 2.8% | ||
| sawyn | 0 | 664,157,771 | 2.8% | ||
| petertag | 0 | 530,351,574 | 4.2% | ||
| calebotamus | 0 | 4,010,181,536 | 100% | ||
| meanbees | 0 | 12,990,129,854 | 10% | ||
| michaelwrites | 0 | 932,338,427 | 35% | ||
| primersion | 0 | 281,768,427,701 | 20% | ||
| deholt | 0 | 4,064,815,032 | 59.5% | ||
| anneporter | 0 | 2,741,269,934 | 21% | ||
| steem.services | 0 | 1,029,094,632 | 1.12% | ||
| diabonua | 0 | 5,207,925,191 | 2.8% | ||
| minerthreat | 0 | 3,653,974,498 | 2.8% | ||
| aliriera | 0 | 8,575,610,801 | 100% | ||
| stevenwood | 0 | 2,991,734,840 | 1.86% | ||
| temitayo-pelumi | 0 | 4,185,390,070 | 50% | ||
| gmlgang | 0 | 486,657,249 | 88% | ||
| andrick | 0 | 827,698,069 | 50% | ||
| motherofalegend | 0 | 8,639,364,002 | 35% | ||
| carilinger | 0 | 102,980,778,505 | 14% | ||
| doctor-cog-diss | 0 | 54,036,245,753 | 70% | ||
| trisolaran | 0 | 1,572,957,951 | 2.8% | ||
| realkiki85 | 0 | 4,961,457,097 | 100% | ||
| marcuz | 0 | 2,350,772,473 | 35% | ||
| acont | 0 | 18,751,682,719 | 50% | ||
| uche-nna | 0 | 103,744,096,390 | 100% | ||
| drawmeaship | 0 | 9,302,887,326 | 50% | ||
| vietthuy | 0 | 811,265,887 | 50% | ||
| we-are-lucky | 0 | 246,847,120 | 0.8% | ||
| letenebreux | 0 | 1,250,265,761 | 33% | ||
| cheese4ead | 0 | 4,110,389,536 | 2.8% | ||
| gaottantacinque | 0 | 86,001,730 | 100% | ||
| carolinaelly | 0 | 2,664,720,800 | 100% | ||
| nathyortiz | 0 | 858,122,607 | 2.8% | ||
| nattybongo | 0 | 19,805,713,974 | 70% | ||
| drsensor | 0 | 1,572,665,910 | 56% | ||
| talentclub | 0 | 7,359,499,562 | 3.36% | ||
| roozeec | 0 | 493,226,385 | 10% | ||
| carl05 | 0 | 655,956,874 | 3.75% | ||
| tanita249 | 0 | 488,092,254 | 100% | ||
| ilovecryptopl | 0 | 922,449,161 | 4.48% | ||
| purelyscience | 0 | 536,710,580 | 35% | ||
| esteliopadilla | 0 | 2,026,440,949 | 100% | ||
| bflanagin | 0 | 6,288,090,749 | 2.8% | ||
| armandosodano | 0 | 12,594,278,890 | 2.8% | ||
| melor9 | 0 | 484,020,776 | 2.8% | ||
| yourmind | 0 | 14,715,754,971 | 100% | ||
| acousticguitar | 0 | 14,154,917,386 | 50% | ||
| marivic10 | 0 | 772,520,848 | 1.4% | ||
| gerdtrudroepke | 0 | 73,244,717,195 | 49% | ||
| zuerich | 0 | 1,980,792,511,019 | 41% | ||
| bambinaacida | 0 | 2,329,807,003 | 50% | ||
| vixmemon | 0 | 1,710,572,652 | 4.2% | ||
| honeycup-waters | 0 | 611,324,173 | 2.8% | ||
| yaelg | 0 | 1,172,042,807 | 1.68% | ||
| minuetoacademy | 0 | 480,359,956 | 5.6% | ||
| kylealex | 0 | 4,590,609,134 | 10% | ||
| gasaeightyfive | 0 | 310,145,641 | 100% | ||
| dlike | 0 | 7,252,898,874 | 3% | ||
| cubapl | 0 | 3,579,123,863 | 30% | ||
| orlandogonzalez | 0 | 3,181,542,946 | 25% | ||
| voxmortis | 0 | 11,165,200,348 | 6% | ||
| fran.frey | 0 | 4,034,535,177 | 50% | ||
| scienceblocks | 0 | 23,591,968,787 | 100% | ||
| perpetuum-lynx | 0 | 2,160,553,777 | 68.6% | ||
| jrevilla | 0 | 1,015,655,394 | 100% | ||
| hanshotfirst-sm | 0 | 490,496,943 | 5.6% | ||
| thelittlebank | 0 | 21,692,277,917 | 2.8% | ||
| pboulet | 0 | 109,649,230,055 | 56% | ||
| javyeslava.photo | 0 | 697,841,551 | 2.24% | ||
| cercle | 0 | 1,134,879,330 | 33% | ||
| josesalazar200 | 0 | 714,203,706 | 5.6% | ||
| a-bot | 0 | 12,520,404,443 | 30% | ||
| stem-espanol | 0 | 18,629,815,889 | 100% | ||
| voter001 | 0 | 2,037,255,524 | 2.5% | ||
| voter002 | 0 | 7,522,056,613 | 20.3% | ||
| voter003 | 0 | 94,483,694,866 | 45.4% | ||
| cribbio | 0 | 461,217,900 | 100% | ||
| cliffagreen | 0 | 4,477,988,383 | 10% | ||
| aleestra | 0 | 11,884,426,478 | 80% | ||
| palasatenea | 0 | 2,794,325,335 | 2.8% | ||
| the.success.club | 0 | 3,204,743,937 | 2.8% | ||
| javier.dejuan | 0 | 540,482,171 | 70% | ||
| xmauron3 | 0 | 1,394,799,532 | 2.8% | ||
| sincensura | 0 | 1,032,664,403 | 100% | ||
| meanroosterfarm | 0 | 1,403,931,540 | 35% | ||
| agrovision | 0 | 570,490,018 | 35% | ||
| teemike | 0 | 815,405,567 | 50% | ||
| merlin7 | 0 | 11,282,749,453 | 5.6% | ||
| brianoflondon | 0 | 26,109,486,026 | 0.84% | ||
| giulyfarci52 | 0 | 1,648,138,112 | 50% | ||
| esthersanchez | 0 | 3,843,703,632 | 60% | ||
| kristall97 | 0 | 24,254,637,462 | 100% | ||
| cwow2 | 0 | 5,620,119,451 | 2% | ||
| steemcryptosicko | 0 | 11,292,116,898 | 1.12% | ||
| certain | 0 | 1,005,787,613 | 0.66% | ||
| alvin0617 | 0 | 493,755,376 | 2.8% | ||
| multifacetas | 0 | 962,739,670 | 2.8% | ||
| cakemonster | 0 | 1,303,912,826 | 1.5% | ||
| cowpatty | 0 | 1,476,048,598 | 35% | ||
| stem.witness | 0 | 4,159,335,368 | 70% | ||
| witkowskipawel | 0 | 948,623,792 | 2.8% | ||
| hiddendragon | 0 | 634,967,270 | 38% | ||
| theskmeister | 0 | 518,783,285 | 100% | ||
| autobodhi | 0 | 993,369,352 | 5.6% | ||
| morarnagringa | 0 | 1,229,288,399 | 100% | ||
| robmojo | 0 | 600,158,909 | 7% | ||
| solox | 0 | 1,017,586,243 | 5.6% | ||
| double-negative | 0 | 523,725,382 | 20% | ||
| shainemata | 0 | 8,312,649,828 | 5% | ||
| wilmer14molina | 0 | 629,664,621 | 50% | ||
| priyandaily | 0 | 4,313,156,401 | 40% | ||
| kork75 | 0 | 824,529,554 | 5.6% | ||
| jacuzzi | 0 | 767,221,351 | 0.84% | ||
| vaultec | 0 | 3,813,181,543 | 12% | ||
| aqua.nano | 0 | 722,732,553 | 35% | ||
| steemegg | 0 | 1,020,610,009 | 2.8% | ||
| ragnarhewins90 | 0 | 495,373,737 | 10% | ||
| jtm.support | 0 | 5,471,624,750 | 70% | ||
| edithbdraw | 0 | 664,419,288 | 2.8% | ||
| crowdwitness | 0 | 58,573,568,161 | 35% | ||
| markwannabee | 0 | 489,984,190 | 100% | ||
| hairgistix | 0 | 3,165,476,352 | 2.8% | ||
| limka | 0 | 123,074,205 | 98.76% | ||
| peter-bot | 0 | 686,431,729 | 100% | ||
| bluemaskman | 0 | 625,870,780 | 2.8% | ||
| steemean | 0 | 10,009,753,304 | 5% | ||
| proxy-pal | 0 | 1,208,303,144 | 5.6% | ||
| quentinvb | 0 | 489,907,365 | 100% | ||
| deveney | 0 | 487,346,796 | 100% | ||
| deriyon | 0 | 488,443,696 | 100% | ||
| thelogicaldude | 0 | 1,059,211,535 | 1.12% | ||
| kggymlife | 0 | 3,460,353,245 | 20% | ||
| medro-martin | 0 | 12,076,913,777 | 95% | ||
| aaronkroeblinger | 0 | 105,467,967,004 | 50% | ||
| projectdignity | 0 | 2,107,876,074 | 96.6% | ||
| jackramsey | 0 | 829,688,172 | 3.92% | ||
| filosof103 | 0 | 878,952,284 | 2.8% | ||
| elements5 | 0 | 2,016,117,138 | 2.8% | ||
| photographercr | 0 | 2,529,237,153 | 1.12% | ||
| larsito | 0 | 9,688,086,607 | 60% | ||
| epicdice | 0 | 1,875,735,544 | 1.68% | ||
| edencourage | 0 | 6,360,069,198 | 50% | ||
| robibasa | 0 | 26,628,359,408 | 10% | ||
| beerlover | 0 | 2,011,684,458 | 1.68% | ||
| qwerrie | 0 | 4,016,553,231 | 0.5% | ||
| tinyhousecryptos | 0 | 487,023,160 | 5% | ||
| steemincome | 0 | 514,325,838 | 7.5% | ||
| rtron86 | 0 | 4,518,597,137 | 50% | ||
| tggr | 0 | 1,308,881,446 | 2.8% | ||
| aicu | 0 | 43,503,438,152 | 5.6% | ||
| zeruxanime | 0 | 11,406,632,391 | 35% | ||
| afarina46 | 0 | 1,950,435,249 | 35% | ||
| hutty | 0 | 3,635,363,132 | 100% | ||
| imbartley | 0 | 812,876,566 | 26.25% | ||
| mind.force | 0 | 1,229,480,817 | 1.4% | ||
| steem.leo | 0 | 2,182,385,496 | 3% | ||
| partitura.stem | 0 | 308,501,519 | 100% | ||
| aicoding | 0 | 577,752,053 | 2.8% | ||
| capp | 0 | 8,134,252,406 | 50% | ||
| beta500 | 0 | 2,972,591,927 | 3% | ||
| dechuck | 0 | 24,713,102,408 | 70% | ||
| bastionpm | 0 | 680,343,264 | 33% | ||
| nazer | 0 | 2,646,960,934 | 35% | ||
| wanderingmoon | 0 | 3,029,465,308 | 50% | ||
| precarious | 0 | 489,061,203 | 50% | ||
| entrepreneur.one | 0 | 3,721,064,487 | 100% | ||
| steemstem-trig | 0 | 5,712,258,963 | 70% | ||
| baltai | 0 | 10,988,598,738 | 2.8% | ||
| atheistrepublic | 0 | 5,692,192,249 | 2.8% | ||
| huaren.news | 0 | 5,539,336,356 | 100% | ||
| ibt-survival | 0 | 34,851,220,794 | 10% | ||
| riazud | 0 | 1,420,778,921 | 2.8% | ||
| xerxes.alpha | 0 | 3,148,416,222 | 100% | ||
| hjmarseille | 0 | 2,168,372,563 | 49% | ||
| roamingsparrow | 0 | 2,564,345,040 | 4.2% | ||
| steemdiamond | 0 | 719,654,050 | 5.6% | ||
| dalz2 | 0 | 1,006,327,418 | 100% | ||
| abachon | 0 | 1,731,023,135 | 5.6% | ||
| zirky | 0 | 2,324,411,480 | 4.76% | ||
| ribary | 0 | 1,041,208,639 | 1.5% | ||
| manic.calm | 0 | 10,142,479,473 | 100% | ||
| mice-k | 0 | 123,104,482 | 3% | ||
| peterale | 0 | 3,247,860,955 | 2.8% | ||
| hive-127039 | 0 | 492,649,525 | 25% | ||
| fengchao | 0 | 72,770,601,891 | 5% | ||
| fsm-core | 0 | 11,170,438,719 | 50% | ||
| hivebuzz | 0 | 10,414,980,011 | 2% | ||
| educationhive | 0 | 1,707,063,998 | 2.8% | ||
| stemsocial | 0 | 616,208,247,012 | 70% | ||
| greenforever | 0 | 1,839,009,839 | 30% | ||
| juniorgomez | 0 | 1,035,997,072 | 15% | ||
| kodeblaccc | 0 | 1,045,715,870 | 2.8% | ||
| peterpanpan | 0 | 867,045,141 | 1.12% | ||
| dcityrewards | 0 | 25,406,887,366 | 3% | ||
| holoferncro | 0 | 2,203,274,639 | 5% | ||
| hiveonboard | 0 | 3,643,465,399 | 2.8% | ||
| louis00334 | 0 | 2,093,935,373 | 50% | ||
| hive-143869 | 0 | 464,140,469,198 | 33% | ||
| noelyss | 0 | 22,189,508,792 | 35% | ||
| schmidi | 0 | 2,417,739,026 | 2.52% | ||
| jsalvage | 0 | 1,048,228,466 | 35% | ||
| life-timer | 0 | 592,302,354,094 | 7.5% | ||
| quinnertronics | 0 | 17,067,730,248 | 8% | ||
| buildahouse | 0 | 902,635,271 | 33% | ||
| anafae | 0 | 571,176,167 | 1.12% | ||
| hivecoffee | 0 | 678,978,411 | 5.6% | ||
| gohive | 0 | 13,548,162,667 | 100% | ||
| sevenoh-fiveoh | 0 | 905,781,353 | 2.8% | ||
| treefiddybruh | 0 | 1,589,608,072 | 2.8% | ||
| aabcent | 0 | 12,584,768,466 | 4.48% | ||
| hive-world | 0 | 660,884,273 | 2.8% | ||
| artsyproxy | 0 | 26,501,441,738 | 5.6% | ||
| altleft | 0 | 22,695,021,492 | 0.05% | ||
| noalys | 0 | 919,886,971 | 2.8% | ||
| evagavilan2 | 0 | 774,669,984 | 2.8% | ||
| apendix1994 | 0 | 3,664,375,681 | 90% | ||
| koshwe | 0 | 1,695,492,020 | 50% | ||
| chubb149 | 0 | 1,879,725,068 | 8.4% | ||
| cosplay.hadr | 0 | 1,240,408,440 | 5.6% | ||
| hadrgames | 0 | 1,276,395,597 | 5.6% | ||
| rawecz | 0 | 591,925,749 | 5.6% | ||
| maar | 0 | 667,170,753 | 70% | ||
| bubblegif | 0 | 2,010,296,004 | 2.8% | ||
| emeraldtiger | 0 | 1,698,724,024 | 16.5% | ||
| meritocracy | 0 | 62,135,298,871 | 0.56% | ||
| eumorrell | 0 | 2,409,749,305 | 100% | ||
| dcrops | 0 | 20,890,789,695 | 1.5% | ||
| entraide.rewards | 0 | 1,094,665,727 | 33% | ||
| traderhive | 0 | 13,058,644,802 | 5.6% | ||
| cookaiss | 0 | 2,698,319,317 | 16.5% | ||
| tawadak24 | 0 | 1,623,561,121 | 2.8% | ||
| eturnerx-honey | 0 | 232,613,431 | 0.8% | ||
| ausbit.dev | 0 | 513,462,345 | 2.8% | ||
| limn | 0 | 811,842,244 | 2.8% | ||
| wynella | 0 | 1,059,580,106 | 2.8% | ||
| dodovietnam | 0 | 2,528,853,855 | 2.8% | ||
| mayorkeys | 0 | 4,910,436,384 | 30% | ||
| oahb132 | 0 | 1,358,953,846 | 35% | ||
| failingforwards | 0 | 3,062,443,137 | 2.8% | ||
| drricksanchez | 0 | 13,686,458,575 | 2.8% | ||
| joseluis91 | 0 | 825,006,086 | 5.6% | ||
| miroslaviv | 0 | 2,225,428,922 | 2.8% | ||
| m0rt0nmattd | 0 | 2,152,244,316 | 100% | ||
| maxelitereturned | 0 | 1,317,795,003 | 35% | ||
| high8125theta | 0 | 8,136,479,614 | 60% | ||
| trippymane | 0 | 1,747,734,913 | 5.6% | ||
| nfttunz | 0 | 9,039,706,924 | 0.56% | ||
| milagrosmhbl | 0 | 5,227,416,920 | 50% | ||
| luisestaba23 | 0 | 487,187,461 | 50% | ||
| hubeyma | 0 | 939,433,162 | 2.8% | ||
| mirteg | 0 | 1,846,988,162 | 5.6% | ||
| podping | 0 | 4,720,883,481 | 0.84% | ||
| drhueso | 0 | 1,324,181,019 | 2.8% | ||
| annafenix | 0 | 506,306,618 | 2.8% | ||
| ayee11 | 0 | 1,113,301,387 | 100% | ||
| mayberlys | 0 | 2,127,947,937 | 50% | ||
| pishio | 0 | 554,352,615,137 | 10% | ||
| jaydr | 0 | 647,826,840 | 2.8% | ||
| chessbrotherspro | 0 | 260,896,038,329 | 100% | ||
| laviesm | 0 | 5,781,818,652 | 50% | ||
| seinkalar | 0 | 3,870,025,577 | 5.6% | ||
| badge-646464 | 0 | 662,027,008 | 5.6% | ||
| sidalim88 | 0 | 2,483,971,283 | 2.8% | ||
| torz18 | 0 | 3,218,726,369 | 100% | ||
| aries90 | 0 | 44,610,563,936 | 5.6% | ||
| finch97 | 0 | 15,562,377,738 | 100% | ||
| onewolfe | 0 | 488,050,602 | 25% | ||
| rencongland | 0 | 563,113,374 | 2.8% | ||
| cugel | 0 | 1,544,830,772 | 2.8% | ||
| martinthemass | 0 | 550,875,895 | 100% | ||
| acantoni | 0 | 871,937,513 | 2.8% | ||
| migka | 0 | 3,951,545,876 | 90% | ||
| pogier | 0 | 2,277,220,612 | 100% | ||
| iradeorum | 0 | 539,387,225 | 100% | ||
| lowelonerf | 0 | 489,693,034 | 100% | ||
| kingz1337 | 0 | 527,377,247 | 100% | ||
| blurtyield | 0 | 94,558,255,316 | 100% | ||
| tony1294 | 0 | 3,891,051,465 | 100% | ||
| rosmarly | 0 | 8,080,873,549 | 100% | ||
| h3m4n7 | 0 | 659,579,492 | 2.8% | ||
| mistural | 0 | 766,738,308 | 5.6% | ||
| yixn | 0 | 13,299,222,498 | 2.8% | ||
| kqaosphreak | 0 | 4,368,917,879 | 70% | ||
| waivio.curator | 0 | 2,517,183,493 | 4.77% | ||
| pzwinz | 0 | 1,196,213,962 | 100% | ||
| simsahas | 0 | 1,141,792,281 | 5.6% | ||
| iumac03 | 0 | 699,065,620 | 2.8% | ||
| ehizgabriel | 0 | 708,013,591 | 35% | ||
| skimanner | 0 | 17,091,241,341 | 100% | ||
| crypt0gnome | 0 | 8,611,147,659 | 1% | ||
| invest-time | 0 | 5,007,440,122 | 100% | ||
| checkyzk | 0 | 45,684,934,003 | 98% | ||
| zzz.accounting | 0 | 2,942,711,730 | 100% | ||
| oabreuf24 | 0 | 7,580,627,275 | 100% | ||
| alexanderalexis | 0 | 16,063,405,145 | 100% | ||
| sam9999 | 0 | 6,296,893,029 | 100% | ||
| benwickenton | 0 | 2,537,863,946 | 5.6% | ||
| dyptre | 0 | 767,363,052 | 2.8% | ||
| synergie | 0 | 3,273,761,734 | 100% | ||
| killerwot | 0 | 2,002,450,619 | 2.8% | ||
| dondido | 0 | 25,229,328,231 | 5.6% | ||
| ydaiznfts | 0 | 788,082,265 | 10% | ||
| arjes | 0 | 7,500,307,406 | 100% | ||
| the420syndicate | 0 | 988,321,345 | 100% | ||
| archangel21 | 0 | 712,962,601 | 5.6% | ||
| ptmaker | 0 | 10,687,373,492 | 50% | ||
| street.curator | 0 | 951,945,980 | 50% | ||
| independance | 0 | 1,123,544,832 | 33% | ||
| mugueto2022 | 0 | 546,270,861 | 20% | ||
| ricardoeloy | 0 | 1,323,654,325 | 14% | ||
| supperbotsps.com | 0 | 566,195,735 | 2.8% | ||
| windail1 | 0 | 610,900,913 | 100% | ||
| nazom | 0 | 1,225,118,043 | 50% | ||
| raca75 | 0 | 625,717,617 | 50% | ||
| theawesononso | 0 | 626,888,004 | 2.8% | ||
| baboz | 0 | 958,432,296 | 1.4% | ||
| mr-rent | 0 | 12,205,096,004 | 75% | ||
| sbtofficial | 0 | 3,795,064,266 | 2.8% | ||
| vagabond42069 | 0 | 1,491,401,560 | 35% | ||
| acgalarza | 0 | 825,400,098 | 0.28% | ||
| inibless | 0 | 3,339,376,093 | 35% | ||
| vragolana | 0 | 729,548,358 | 2.8% | ||
| cindynancy | 0 | 1,166,899,440 | 35% | ||
| gejami | 0 | 4,833,076,841 | 100% | ||
| genepoolrentsclr | 0 | 1,471,015,822 | 2.8% | ||
| sc000 | 0 | 1,377,607,129 | 5.6% | ||
| minava.museum | 0 | 1,114,361,033 | 33% | ||
| lordnight72 | 0 | 1,113,142,062 | 33% | ||
| quotidien | 0 | 2,157,383,162 | 33% | ||
| cardcompounding | 0 | 1,859,005,046 | 100% | ||
| vankushfamily | 0 | 672,478,613 | 35% | ||
| cli4d | 0 | 495,521,086 | 2.24% | ||
| jijisaurart | 0 | 533,230,927 | 2.8% | ||
| tuba777 | 0 | 1,537,851,017 | 35% | ||
| workaholic666 | 0 | 605,442,920 | 100% | ||
| minas-glory | 0 | 5,563,662,811 | 2.8% | ||
| clpacksperiment | 0 | 2,241,973,541 | 2.8% | ||
| the-grandmaster | 0 | 4,722,818,273 | 2.8% | ||
| the-burn | 0 | 5,972,840,821 | 2.8% | ||
| psychophilo | 0 | 953,540,654 | 50% | ||
| alenazaa | 0 | 587,533,739 | 100% | ||
| sapphireleopard | 0 | 568,064,690 | 33% | ||
| superuser3 | 0 | 1,631,484,377 | 35% | ||
| splinterboost | 0 | 36,793,350,354 | 7.5% | ||
| ylaffittep | 0 | 4,108,710,765 | 100% | ||
| hbcpt | 0 | 63,353,293,145 | 50% | ||
| elluismma | 0 | 1,032,052,387 | 100% | ||
| lettinggotech | 0 | 1,300,833,590 | 2.8% |
Interesting. My first 'intuition' was that, since there's 2 doors remaining, they each have a 50% chance of having the car behind them, so it doesn't matter which one I pick. But then I started thinking, if we make it into a rule that the 'talk show host' changes the door randomly after your first choice, then this might influence the chances somehow, though I could not specify how by just superficially thinking about it without math.
| author | alexanderalexis | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| permlink | rqqwei | ||||||||||||
| category | hive-196387 | ||||||||||||
| json_metadata | {"app":"hiveblog/0.1"} | ||||||||||||
| created | 2023-02-27 15:30:18 | ||||||||||||
| last_update | 2023-02-27 15:30:18 | ||||||||||||
| depth | 1 | ||||||||||||
| children | 1 | ||||||||||||
| last_payout | 2023-03-06 15:30:18 | ||||||||||||
| cashout_time | 1969-12-31 23:59:59 | ||||||||||||
| total_payout_value | 0.030 HBD | ||||||||||||
| curator_payout_value | 0.030 HBD | ||||||||||||
| pending_payout_value | 0.000 HBD | ||||||||||||
| promoted | 0.000 HBD | ||||||||||||
| body_length | 438 | ||||||||||||
| author_reputation | 1,916,610,782,909 | ||||||||||||
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" | ||||||||||||
| beneficiaries |
| ||||||||||||
| max_accepted_payout | 1,000,000.000 HBD | ||||||||||||
| percent_hbd | 10,000 | ||||||||||||
| post_id | 121,171,387 | ||||||||||||
| net_rshares | 114,499,238,810 | ||||||||||||
| author_curate_reward | "" |
| voter | weight | wgt% | rshares | pct | time |
|---|---|---|---|---|---|
| alexander.alexis | 0 | 58,681,917,622 | 100% | ||
| cyprianj | 0 | 55,817,321,188 | 100% |
Yeah, if he changes the door randomly, it would have been more complicated than this, and this would then likely involve the application of combinatorics, to calculate the total possible ways for the probability (I might probably not have even bothered racking my brain over such a situation).
| author | cyprianj |
|---|---|
| permlink | re-alexanderalexis-rqr09m |
| category | hive-196387 |
| json_metadata | {"tags":["hive-196387"],"app":"peakd/2023.2.2"} |
| created | 2023-02-27 16:53:45 |
| last_update | 2023-02-27 16:53:45 |
| depth | 2 |
| children | 0 |
| last_payout | 2023-03-06 16:53:45 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 293 |
| author_reputation | 75,398,556,172,423 |
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 121,173,625 |
| net_rshares | 16,376,884,865 |
| author_curate_reward | "" |
| voter | weight | wgt% | rshares | pct | time |
|---|---|---|---|---|---|
| alexanderalexis | 0 | 16,376,884,865 | 100% |
<h3>Congratulations!</h3><hr /><div class="pull-right"><img src="https://images.hive.blog/DQmQLssYuuJP2neoTVUbMRzvAu4Ptg7Vwt92aTM7Z3gNovg/cb-logo-150.png" alt="You have obtained a vote from CHESS BROTHERS PROJECT"/></div><div class="text-justify"><h3>✅ Good job. Your post has been appreciated and has received support from <a href="/@chessbrotherspro"><b>CHESS BROTHERS</b></a> ♔ 💪</h3><p><br>♟ We invite you to use our hashtag <b>#chessbrothers</b> and learn more <a href="/@chessbrotherspro/introducing-chess-brothers-project-the-most-innovative-community-combining-chess-fitness-and-more"><b>about us</b></a>.</p><p>♟♟ You can also reach us on our <a href="https://discord.gg/73sK9ZTGqJ" rel="noopener" title="This is going to take you to the Discord of Chess Brothers"><b>Discord server</b></a> and promote your posts there.</p><p>♟♟♟ Consider <a href="/@chessbrotherspro/teamwork-is-worthwhile-join-the-chess-brothers-healing-trail-supporting-the-work-being-done-and-earning-rewards"><b>joining our curation trail</b></a> so we work as a team and you get rewards automatically.</p><p>♞♟ Check out our <a href="/@chessbrotherspro"><b>@chessbrotherspro</b></a> account to learn about the curation process carried out daily by our team.</p><p><br>🏅 If you want to earn profits with your HP delegation and support our project, we invite you to join the <i>Master Investor</i> plan. <a href='/@chessbrotherspro/master-investor-plan-or-programa'>Here you can learn how to do it.</a></p></div><div class="text-center"><p><br>Kindly</p><p><strong><em>The CHESS BROTHERS team</em></strong></p></div>
| author | chessbrotherspro |
|---|---|
| permlink | re-the-monthy-hall-paradox-a-clearer-understanding-of-the-game-the-idea-and-the-logic-behind-it |
| category | hive-196387 |
| json_metadata | "" |
| created | 2023-02-26 13:37:00 |
| last_update | 2023-02-26 13:37:00 |
| depth | 1 |
| children | 0 |
| last_payout | 2023-03-05 13:37:00 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 1,598 |
| author_reputation | 78,769,948,807,885 |
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 121,138,625 |
| net_rshares | 0 |
<center> *This post has been given a 7.5% UpVote by the SplinterBoost Community Curation Bot.* </center><center>  </center><center> [Vote For Witness ](https://vote.hive.uno/@splinterboost) | [Delegate HP](https://peakd.com/@splinterboost) | [Join Discord](https://discord.gg/RK4ZHKmgcX) </center>
| author | splinterboost |
|---|---|
| permlink | 5,806,027,227 |
| category | hive-196387 |
| json_metadata | "{"tags": ["science", "splinterlands", "discovery-it", "appreciator", "neoxian", "curangel", "stemng", "indiaunited", "palnet", "chessbrothers"], "image": ["https://i.imgur.com/7gUumlT.png"]}" |
| created | 2023-02-25 20:50:06 |
| last_update | 2023-02-25 20:50:06 |
| depth | 1 |
| children | 0 |
| last_payout | 2023-03-04 20:50:06 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 343 |
| author_reputation | 13,751,072,041,640 |
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 121,121,066 |
| net_rshares | 0 |
<div class='text-justify'> <div class='pull-left'> <img src='https://stem.openhive.network/images/stemsocialsupport7.png'> </div> Thanks for your contribution to the <a href='/trending/hive-196387'>STEMsocial community</a>. Feel free to join us on <a href='https://discord.gg/9c7pKVD'>discord</a> to get to know the rest of us! Please consider delegating to the @stemsocial account (85% of the curation rewards are returned). Thanks for including @stemsocial as a beneficiary, which gives you stronger support. <br /> <br /> </div>
| author | stemsocial |
|---|---|
| permlink | re-cyprianj-the-monthy-hall-paradox-a-clearer-understanding-of-the-game-the-idea-and-the-logic-behind-it-20230227t041600126z |
| category | hive-196387 |
| json_metadata | {"app":"STEMsocial"} |
| created | 2023-02-27 04:16:00 |
| last_update | 2023-02-27 04:16:00 |
| depth | 1 |
| children | 0 |
| last_payout | 2023-03-06 04:16:00 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 545 |
| author_reputation | 22,930,630,319,843 |
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 121,158,309 |
| net_rshares | 0 |
I'm not a mathematician either so I will take your word for it. I thought it was Monty Hall. 🤔🤔 No I gotta go look it up.
| author | wanderingmoon |
|---|---|
| permlink | re-cyprianj-2023226t10221340z |
| category | hive-196387 |
| json_metadata | {"tags":["science","splinterlands","discovery-it","appreciator","neoxian","curangel","stemng","indiaunited","palnet","chessbrothers"],"app":"ecency/3.0.31-vision","format":"markdown+html"} |
| created | 2023-02-26 16:02:21 |
| last_update | 2023-02-26 16:02:21 |
| depth | 1 |
| children | 3 |
| last_payout | 2023-03-05 16:02:21 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.014 HBD |
| curator_payout_value | 0.015 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 122 |
| author_reputation | 20,955,529,739,902 |
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 121,141,843 |
| net_rshares | 56,084,421,029 |
| author_curate_reward | "" |
| voter | weight | wgt% | rshares | pct | time |
|---|---|---|---|---|---|
| cyprianj | 0 | 56,084,421,029 | 100% |
Oh my.... how did I make this mistake. You are right. It's Monty and not Monthy. Thank you for this.
| author | cyprianj |
|---|---|
| permlink | re-wanderingmoon-rqq2gs |
| category | hive-196387 |
| json_metadata | {"tags":["hive-196387"],"app":"peakd/2023.2.2"} |
| created | 2023-02-27 04:43:39 |
| last_update | 2023-02-27 04:43:39 |
| depth | 2 |
| children | 2 |
| last_payout | 2023-03-06 04:43:39 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.000 HBD |
| curator_payout_value | 0.000 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 100 |
| author_reputation | 75,398,556,172,423 |
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 121,158,755 |
| net_rshares | 1,440,889,308 |
| author_curate_reward | "" |
| voter | weight | wgt% | rshares | pct | time |
|---|---|---|---|---|---|
| wanderingmoon | 0 | 1,440,889,308 | 25% |
It happens to the best of us. 😁
| author | wanderingmoon |
|---|---|
| permlink | re-cyprianj-rqq4vn |
| category | hive-196387 |
| json_metadata | {"tags":["hive-196387"],"app":"peakd/2023.2.2"} |
| created | 2023-02-27 05:35:48 |
| last_update | 2023-02-27 05:35:48 |
| depth | 3 |
| children | 1 |
| last_payout | 2023-03-06 05:35:48 |
| cashout_time | 1969-12-31 23:59:59 |
| total_payout_value | 0.014 HBD |
| curator_payout_value | 0.014 HBD |
| pending_payout_value | 0.000 HBD |
| promoted | 0.000 HBD |
| body_length | 31 |
| author_reputation | 20,955,529,739,902 |
| root_title | "The Monty Hall paradox: A clearer understanding of the game, the idea, and the logic behind it" |
| beneficiaries | [] |
| max_accepted_payout | 1,000,000.000 HBD |
| percent_hbd | 10,000 |
| post_id | 121,159,752 |
| net_rshares | 54,731,811,381 |
| author_curate_reward | "" |
| voter | weight | wgt% | rshares | pct | time |
|---|---|---|---|---|---|
| cyprianj | 0 | 54,731,811,381 | 100% |
 hiveblocks
hiveblocks